author:	sritank
score:	10 / 10

TODO: Summarize the paper:

• Main idea
• Adaptively change the learning rate in a way that it reduces oscillations i.e. slows down close to minimas, and is large otherwise.
• Change step size based on the windowed accumulated gradient and also accumulated step sizes, which only require 1st order computations.
• Windowed accumulation makes sure updates after multiple iterations aren’t drowned out by massive accumulated denominator like in ADAGRAD

• Scaling the step size by the accumulated previous step sizes gives it the correct units, as if it were a 2nd order adaptive method

• Technical implementation
• Scaling gradient helps ensure we take an equal step in all directions
• Builds on ADAGRAD which scales the learning rate based on the accumulated sum of previous gradients.

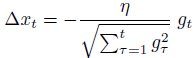
• By choosing an exponential decaying average for accumulating the gradient they solved the 0 step size problem of ADAGRAD

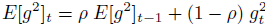
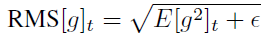where epsilon is used to condition the denominator for numerical purposes.

• By assuming locally smooth curvature, they scaled up the step size using the exponentially decaying average of previous step sizes.

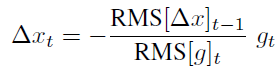
• Algorithm performance
• numerator RMS term lags behind the denominator by 1 time step, making it robust to large sudden gradients. Denominator increases slowing down the progress before numerator can blow up.
• The method makes approximations on Hessian and local curvature, giving it second order characteristics while still costing only one gradient computation per iteration.
• In experiments, the training method is used on DNNs with sigmoid and ReLU units. The DNNs were trained for MNIST classification and speech recognition.

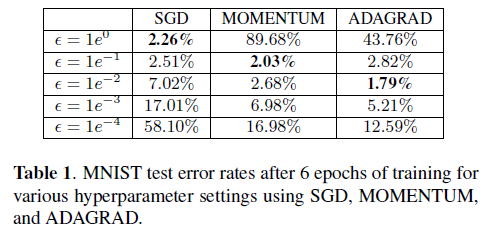
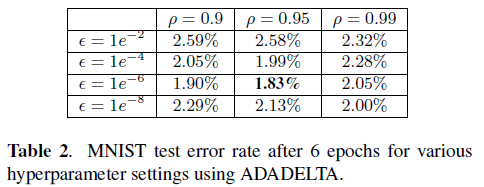
• ADADELTA is less sensitive to hyperparameter settings compared to other methods and converges quickly.
• The lower layer gradients are larger than top layer gradients indicating that ADADELTA doesn’t suffer from diminishing gradient problem (also tackles vanishing gradient in tanh network).
• Step size converges to a constant at the end of training resulting in parameter updates converging to zero (gradients become too small). Acts as if annealing schedule is present.
• For Audio signal classification, ADADELTA converged faster than other methods even under circumstances where accumulated gradients had significant noise.

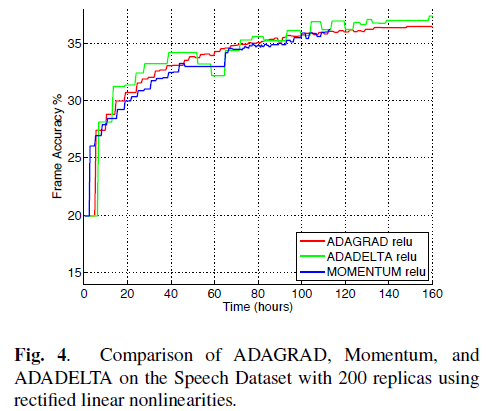
TL;DR

• New adaptive learning rate algorithm (ADADELTA) is introduced and it has first order computational cost
• ADADELTA is more robust to choice of hyperparameters used and converges smoothly and faster than other learning rates
• ADADELTA doesn’t suffer from diminishing gradient problem for cases tested in the paper and exhibits characteristics of second order learning rates