Linformer: Self-Attention with Linear Complexity, Wang, Li, Khabsa, Fang, Ma; 2020 - Summary
author: Jordi
score: 8 / 10

This paper introduces a linear transformer, the Linformer, performs on par with standard Transformer models, while being much more memory- and time-efficient. It suggests an approximate way of calculating self-attention in Transformer architectures that has linear space and time complexity in terms of the sequence length, with the resulting performance on benchmark datasets similar to that of the RoBERTa model based on the original Transformers with much less efficient quadratic attention complexity.

The Problem

Transformers are notoriously resource-intensive because their self-attention mechanism requires a squared number of memory and computations O(n^2) in the length of the input sequence.

The Solution

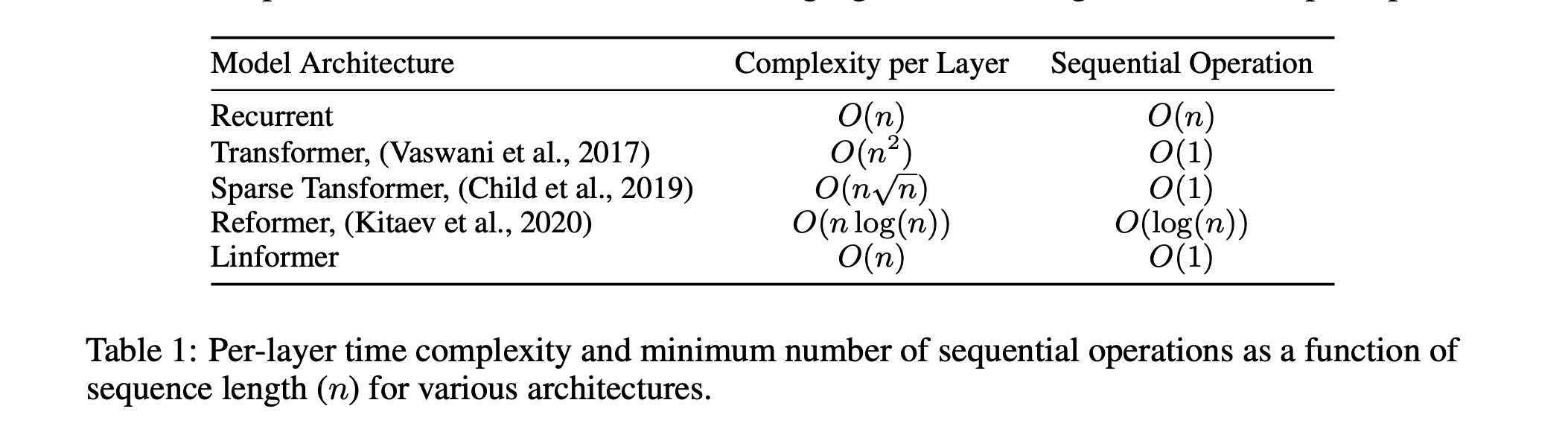The Linformer Model gets around that by using the fact that often, the actual information in the attention matrix is of lower rank and can be approximated.

The implementation

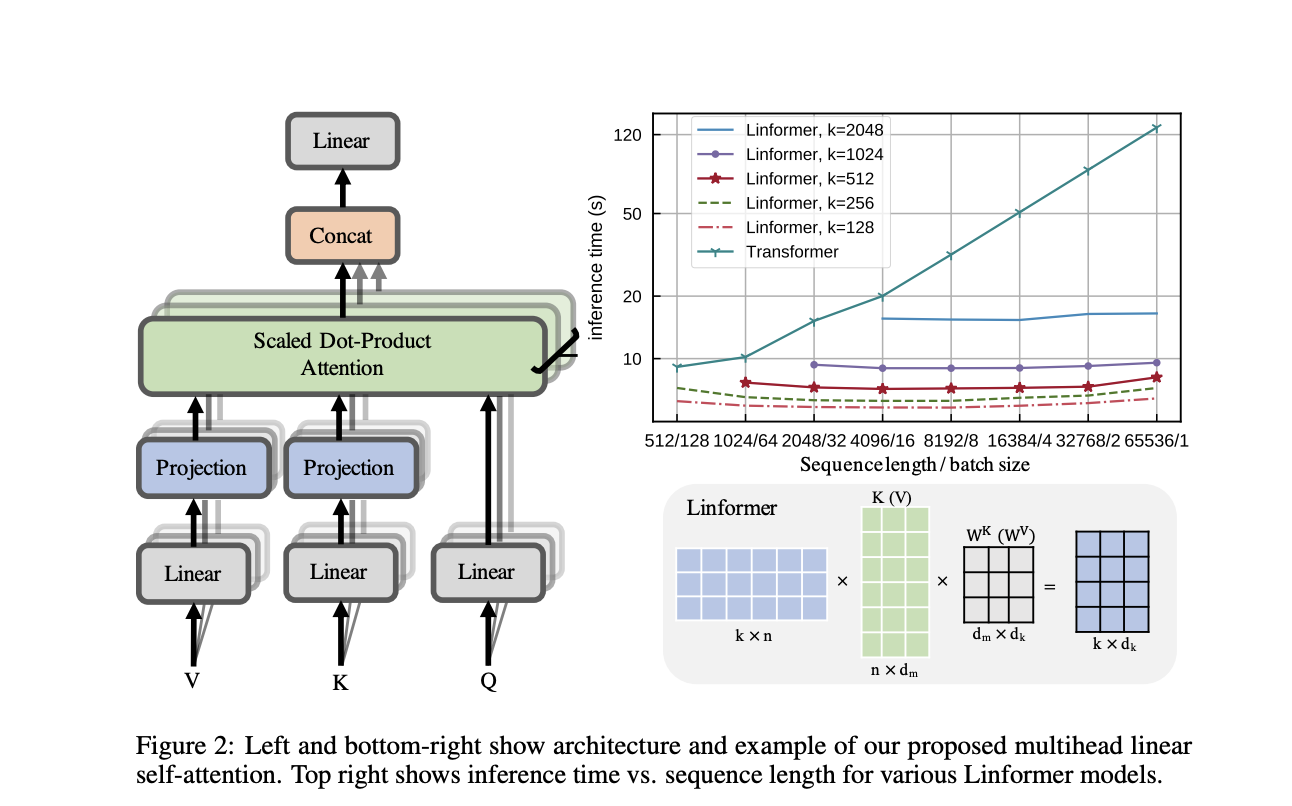In this paper, the authors show both theoretically and empirically that the attention dot product matrix can always be closely approximated by a matrix of much lower rank, which can be obtained by calculating the singular value decomposition (SVD) of the key and value matrices and only using a fixed number of the largest singular values. Since SVD calculation also adds computational complexity, the authors replace it with a linear projection layer (as shown in the picture) that serves to reduce the dimensionality. For simplicity, the trainable projection layer parameters can be shared between attention heads and/or between layers.

The Transformer is built upon the idea of Multi-Head Self-Attention (MHA). MHA is defined as:

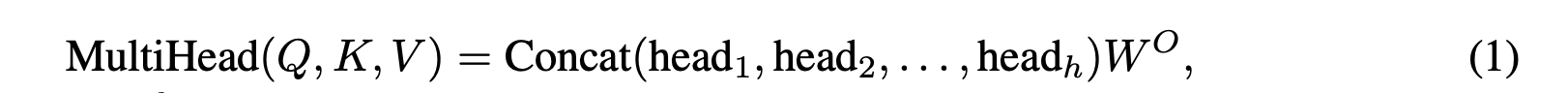
And each head is defined as:

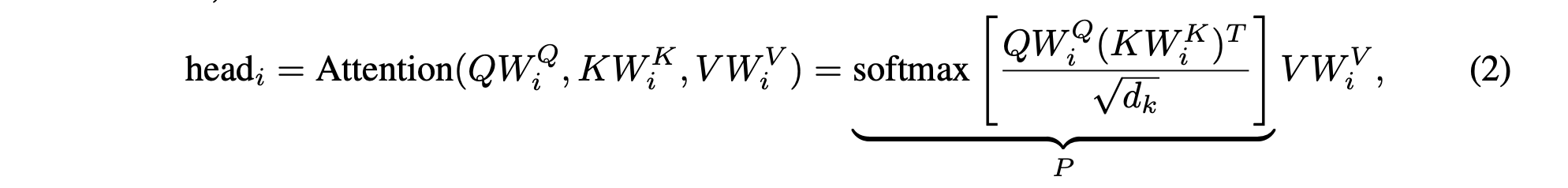
K and V represent the keys and values used in attention. W are learned matrices. The Transformer uses P to capture the input context for a given token and computing P is very expensive which uses O(n^2) time. This paper focus on reducing this to O(n) time by using linear projection.

The paper finally derives:

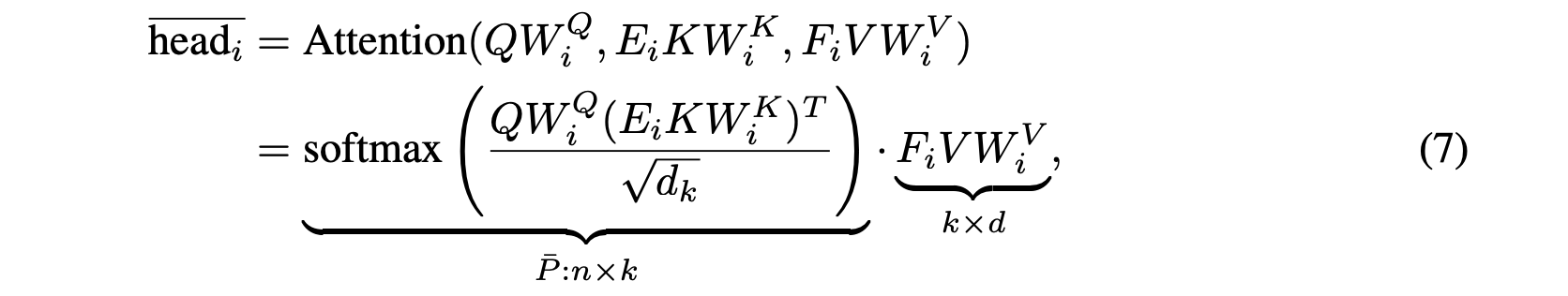
Where it only requires O(nk) time and space complexity.

Additional Efficiency Techniques

Parameter sharing between projections: One can share parameters for the linear projection matrices Ei , Fi across layers and heads.

Nonuniform projected dimension: One can choose a different projected dimension k for different heads and layers.

General projections: One can also choose different kinds of low-dimensional projection methods instead of a simple linear projection.

The Result

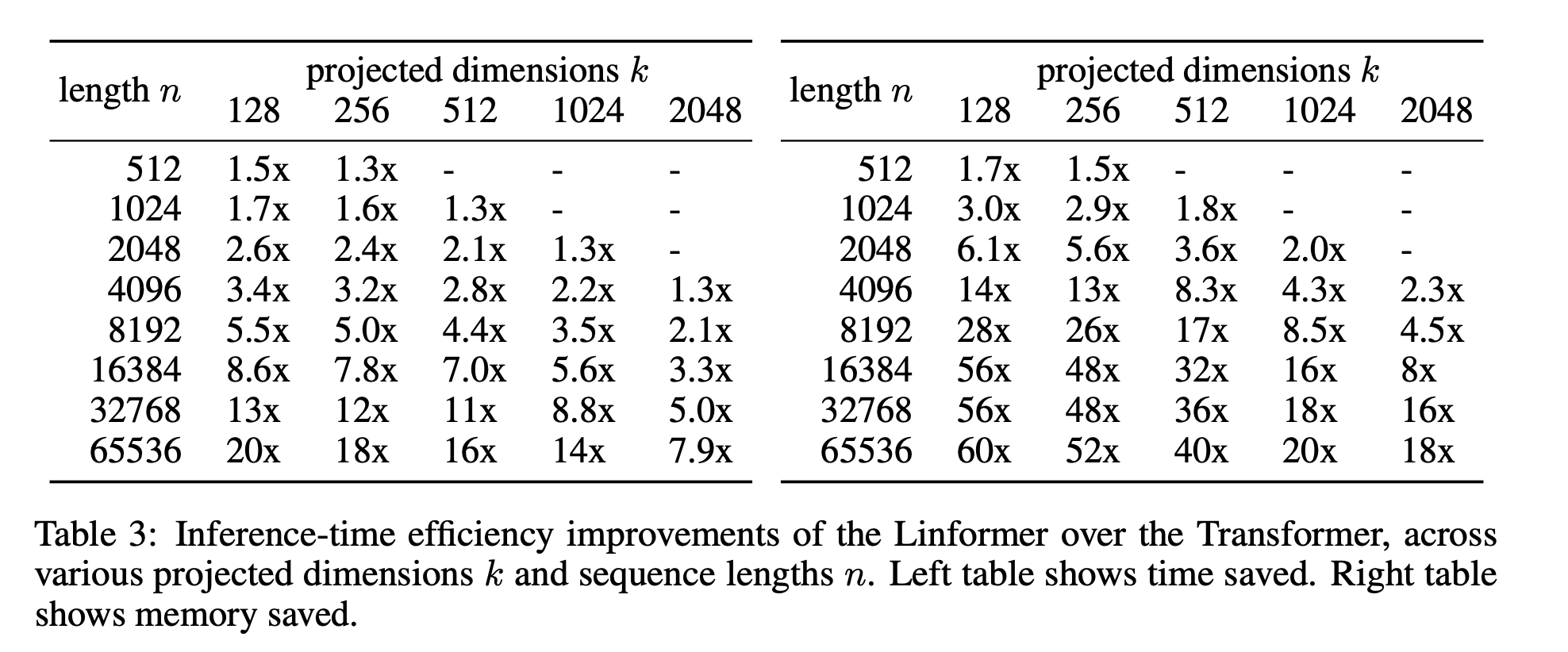
The table above shows the inference efficiencies of linformer (with layerwise sharing) against a standard Transformer. The left table shows time saved while the right table shows memory saved.

It is shown that the performance of both the pre-trained and fine-tuned Linformer models is similar to and sometimes exceeding that of RoBERTa, a popular state-of-the-art BERT variant. At the same time, the inference time speed-up and memory savings can be 20–60 fold for longer sequences.

While the suggested approach still required training on 64 Tesla V100 GPUs, it certainly seems more efficient and thus very promising for using the pre-trained models in downstream applications. Also, as the authors point out, the ability to train on longer sequences creates the potential of training Transformer models on images more easily.

TL;DR