| author: | liaojh1998 |
| score: | 7 / 10 |
Note: LR stands for Learning Rate
-
What is the core idea?
This paper proposes a learning rate policy where the learning rate oscillates between two bounds and a method to estimate the two bounds reasonably.
According to Dauphin et al., 2015, loss is more difficult to minimize due to saddle points rather than poor local minima, and increasing the learning rate allows for more rapid traversal away from saddle points. Also, increasing the learning rate might have short term negative effects but can achieve beneficial effects in the long term. The author showed this when training GoogleNet on ImageNet:

Although the validation accuracy decreased during periods of increasing LR, the accuracy improved with higher gains during periods of decreasing LR. Thus, cyclical LR policy may speed up training to achieve better accuracy in the long run. It also removes the need to guess the optimal LR to use at each timestep in training.
-
How is it realized (technically)?
The author tested multiple functional forms of cyclical LR windows (triangular, Welch (parabolic), Hann (sinusoidal)) and found that they all produced equivalent results. The triangular LR window was the simplest for implementation. Thus, the following triangular LR window was used:

The blue line represents the LR values changing between the
base_lrandmax_lr. Note that thestepsizeis the number of iterations in half a cycle. Thus, forstepsizesteps, LR will increase linearly frombase_lrtomax_lr, and then for anotherstepsizesteps, LR will decrease linearly frommax_lrtobase_lr. This is done in code by adding the necessary amount of LR to thebase_lrfor each step, and use that value as the LR for the step.The author advocated the following guidelines:
-
Good
stepsize: The number of iterations in an epoch is defined as the number of training images divided by thebatchsize. So, if a dataset has 50,000 training images and thebatchsize = 100, there are50000/100 = 500iterations in an epoch. According to experiments, it is often good to setstepsizeequal to 2 to 10 times the number of iterations in an epoch. Note thatstepsizeis half a cycle. -
Good Stopping Point: It is best to stop training at the end of a cycle because that’s when LR is a minimum value and the accuracy peaks. However, it is up to the reader’s discretion how many cycles to use. Experiments found that at least 3 cycles trained the network most of the way, but 4 or more cycles achieved even better performance.
-
Reasonable Minimum and Maximum LR: Do an “LR range test” by running the model for several epochs while increasing the LR from low to high values. Then, plot the accuracy vs. LR of the model like the following:

The maximum value for LR is when accuracy slows, becomes ragged, or starts to fall, like when
lr = 0.006in this case. According to Bengio 2012, the optimum LR is usually within a factor of two of the largest LR that allows the model to converge. Thus, the minimum value for LR can be \(\frac{1}{3}\) or \(\frac{1}{4}\) of the maximum value.
-
-
What interesting variants are explored?
The author proposed two variations of cyclical LR:
-
triangular2: This is same as thetriangularpolicy, but the learning rate difference is cut in half at the end of each cycle like the following: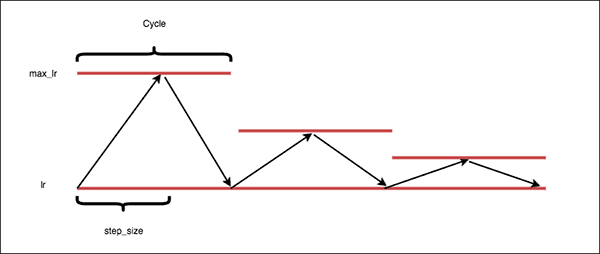
-
exp_range: Similar to thetriangularpolicy, but themax_lrdecreases by an exponential factor of \(\gamma^{\text{iteration}}\) like the following: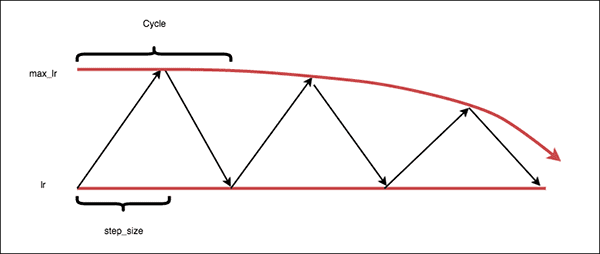
Note that different cyclical LR schedules with different boundary values can be appended one after the other. The author did this on the CIFAR-10 baseline by training it with sequential
triangular2policies with the following boundary values:
-
-
How well does the paper perform?
The author tested the LR schedule on multiple models designed for image classification. They used the CIFAR-10, CIFAR-100, and ImageNet datasets. Generally, the models performed the best when trained with cyclical LR or its variants, averaging about a 0.8% increase in accuracy over a fixed LR schedule. Here’s a summary of comparisons:

For clarifications,
decayis a LR policy with boundary values in where LR starts atmax_lrand is reduced tobase_lrafter some iterations, then the LR is kept atbase_lrfor all iterations after.expis an exponential decay policy for LR.The author notes the following in general:
triangular2policy usually trained the model in less iterations for comparable accuracy. Training longer ontriangular2outperforms training on afixedLR policy.-
Adaptive learning rate methods can combine with cyclical LR to obtain comparable accuracy as shown in the following:

Note that some methods (AdaGrad, AdaDelta) when combined with CLR, while using only 25k iterations of training, still gained a final accuracy that is equivalent to the final accuracy of the method without CLR, which used 70k iterations of training. Refer to the next lecture for explanations on these methods.
-
Training ResNet, Stochastic Depth networks, and DenseNets with cyclical LR performed better than training with a fixed LR by about 0.2% increase in accuracy on average for CIFAR-10 and by about 0.5% increase in accuracy on average for CIFAR-100:

TL;DR
- CLR oscillates the learning rate between a minimum and maximum value during training.
- CLR removes the need to tune an optimal schedule for LR.
- CLR can train the network faster to achieve a better accuracy in the long run.