Implicit Neural Representations with Periodic Activation Functions, Sitzmann, Martel, Bergman, Lindell, Wetzstein; 2020 - Summary
| author: | rll2396 |
| score: | 7 / 10 |
TODO: Summarize the paper:
- Background
- Implicit functions take the form \(F(x, \Phi, \nabla_x\Phi, \nabla_x^2\Phi, \dots) = 0\)
- \(\Phi\) maps \(x\) to some quantity of interest
- e.g. the equation for the unit circle is \(x^2 + \Phi^2 - 1 = 0\)
- Traditional methods for modeling such functions involve discretizing the domain into sections, then numerically solving at each section
- NNs can be used for continuous model
- agnostic to grid resolution
- model memory only scales with complexity of the function, rather than spatial resolution
- common activation functions such as ReLU achieve poor performance
- Implicit functions take the form \(F(x, \Phi, \nabla_x\Phi, \nabla_x^2\Phi, \dots) = 0\)
- What is the core idea?
- Two main contributions
- demonstrate that the sine activation functions works very well for creating implicit neural representations
- create a new initialization technique, which is essential for the performance that they achieve with their network
- Two main contributions
-
How is it realized (technically)?
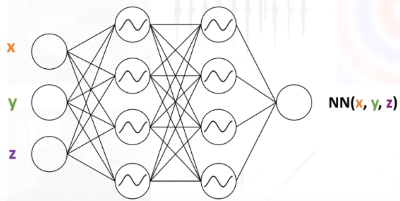
- Implicit equations relate an input, a function, and the function’s derivatives to 0
- \[C_m(x, \Phi(x), \nabla\Phi(x),\dots) = 0\]
- a simple loss function is just the absolute value of the left hand side
- dynamically sample some set of points \(x_i \in \Omega\) at which to evaluate the expression
- \[L = \sum_i^{\Omega}\sum_m ||C_m(x_i, \Phi(x_i), \nabla\Phi(x_i),\dots)||\]
- Sinusoidal representation network (SIREN)
- MLP with sine as the activation function
- derivative of a SIREN is also a SIREN, since the derivative of sine is just a phase shifted sine
- during initialization, weights are drawn from \(U(-\sqrt{\frac{6}{n}},\sqrt{\frac{6}{n}})\)
- \(n\) is input dimension
- For all experiments, they use a 5-layer MLP and optimize it using ADAM with a learning rate of 1e-4
- Implicit equations relate an input, a function, and the function’s derivatives to 0
-
How well does the paper perform?


- Poisson image reconstruction
- SIREN is used to solve the Poisson equation
- goal is to reconstruct an image
- the gradient or Laplacian of the ground truth image is used for supervision
- SIREN does well with both types of supervision
- Both ReLU and Tanh completely fail the reconstruction when supervised with Laplacian
- Poisson image editing
- SIREN is used to create an image from the linear interpolation of the gradients of two images
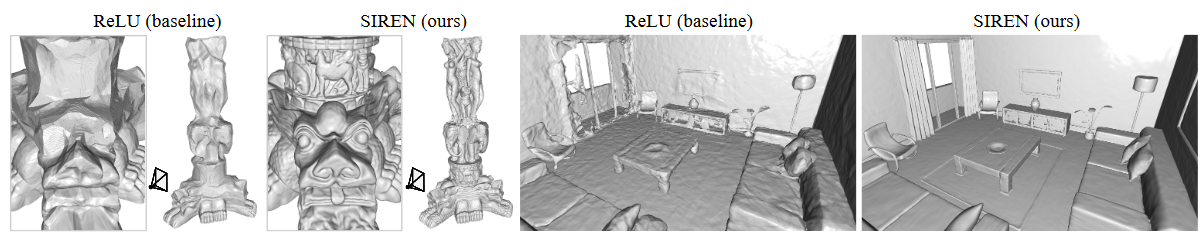
- Representing shapes with signed distance functions
- Inspired by recent work, they decide to use SDFs to fit the network to point clouds
- SDF outputs the distance to the boundary of the shape
- the SDF values are negative when outside the shape and positive when inside the shape
- gradient is \(1\) almost everywhere
- \(\| \|\nabla_x(\Phi(x))\| - 1\|\) for all points
- distance values on the shape should be close to 0
- \(\|\Phi(x)\|\) for all points on the shape
- distance values off the shape should not be close to 0
- \(\exp(-\alpha \cdot \|\Phi(x)\|)\) for all points off the shape
- for calculating loss, sum up these values
- sample random points in the domain, half on the shape half off it

- Helmholtz equation
- Supervise with loss function based on helmholtz equation, which relates the Laplacian of a function with itself
- Network outputs two values to account for complex solutions

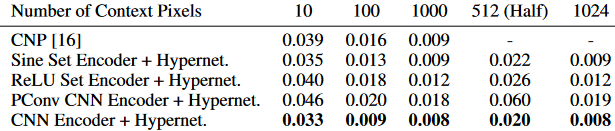
- Learning a space of implicit functions
- convolutional encoder maps partial observations of an image to latent code vectors
- ReLU hypernetwork maps the latent code vectors to SIREN network parameters
- the resulting SIREN can fill in the rest of the image
- works comparably to other methods
- Poisson image reconstruction
TL;DR
- Sine activation functions are effective at describing complex signals and their derivatives
- Requires careful initialization
- Demonstrated to achieve much better performance on a variety of tasks