• What is the core idea?
  • Introduces the Adam (Adaptive Moment Estimation) algorithm.
    • First-order gradient-based optimization of stochastic objective functions
    • Method uses estimates of first and second moments of the gradients to compute individual adaptive learning rates for different parameters
  • What exactly is a moment?
    • an n-th moment (\(m_n\)) is defined as the expteced value of that variable to the power of n, i.e. \(m_n = E[X^n]\)
      • So the first moment is the mean, and the second moment is uncentered variance
  • Advantages:
    • Algorithm based on adaptive estimates
      • This avoids gradient explosion.
    • Computationally efficient
    • Memory efficient
    • Appropriate for problems with very noisy and/or sparse gradients
    • Combines the advantages of AdaGrad and RMSProp
      • Like RMSProp, Adam also keeps a running average of \(v_t\) (see algorithm below).
        • RMSProp lacks a bias correction term
      • AdaGrad and Adam correspond to each other directly when \(\beta_1\) and \(\beta_2\) are carefully chosen in the algortihm below.
    • Includes bias correction to ensure moment estimates do not bias toward 0
  • Disadvantages:
    • Looking back, Adam got people excited with it’s great results (see some below), but does not converge for some tasks - like image classifcaiton on the CIFAR datasets.
    • The proof of convergence in the paper is wrong - prompted another paper which proves the convergence of Adam - An improvement of the convergence proof of the ADAM-Optimizer by Bock et al.
• How is it realized (technically)?
  • 
  • Current \(m_t\) and \(v_t\) keep an expoentially decaying average of past values of \(m_t\) and \(v_t\).
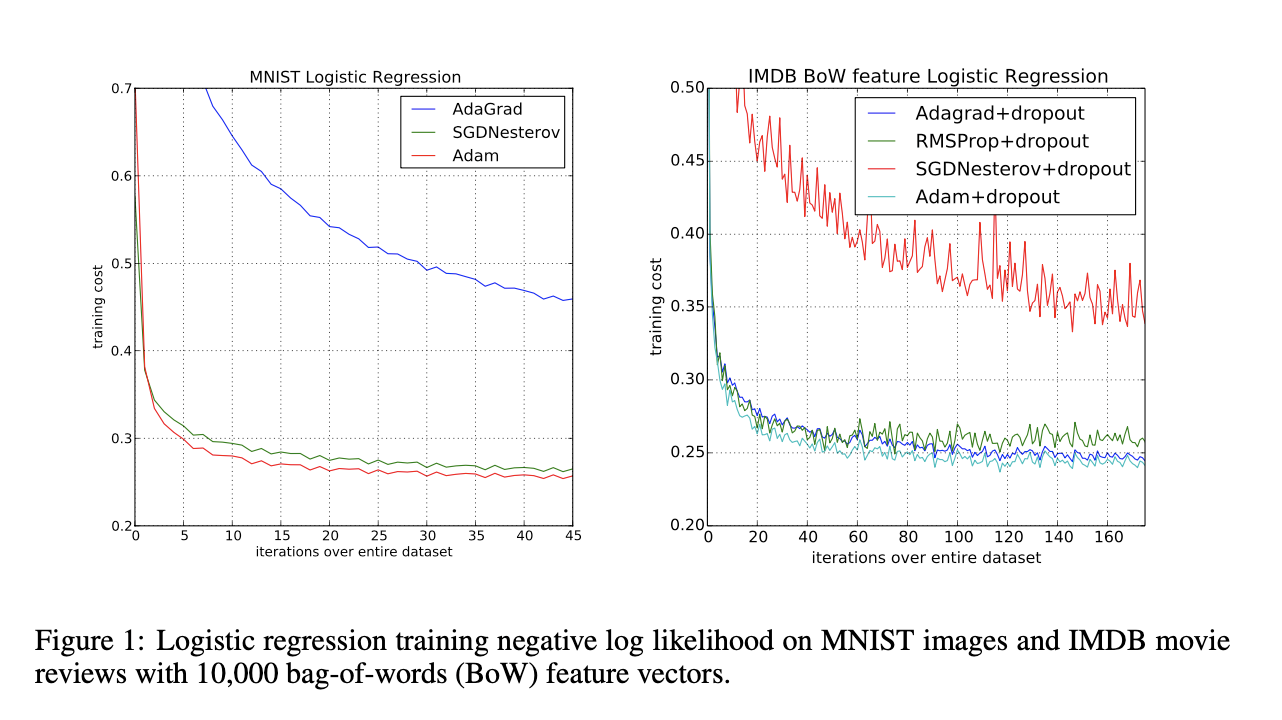
• How well does the paper perform?
  • Very well in the experiments run in the paper.
  • 
• What interesting variants are explored?
  • AdaMax - based on the infinity norm
  • 

TL;DR

• Computationally efficient algorithm that uses adaptive estimation to find individual learning rates for each parameter.
• Really good results in experiments
• Combines the advantages of AdaGrad and RMSProp