What is the core idea?

• Inductive biases are baked into models, thus while increasing efficiency, they limit the model’s performance to one particular modality.

  • Enter Perceiver, a model designed to handle arbitrary configurations of different modalities.

• Perceiver is built upon Transformers

• By introducing a small set of latent units, the authors are able to introduce an attention bottleneck through which inputs must pass.

  • Eliminates the quadratic scaling problem of the classical Transformer
  • Decouples network depth from input’s size

• Allows scaling to hundreds of thousands of inputs like ConvNets

• Employs asymmetric attention mechanism to iteratively distill inputs
  • Hence, can scale to handle very large inputs
• Model is competitive or outperforms strong specialised models across various modalities

How is it realized (technically)?

• 

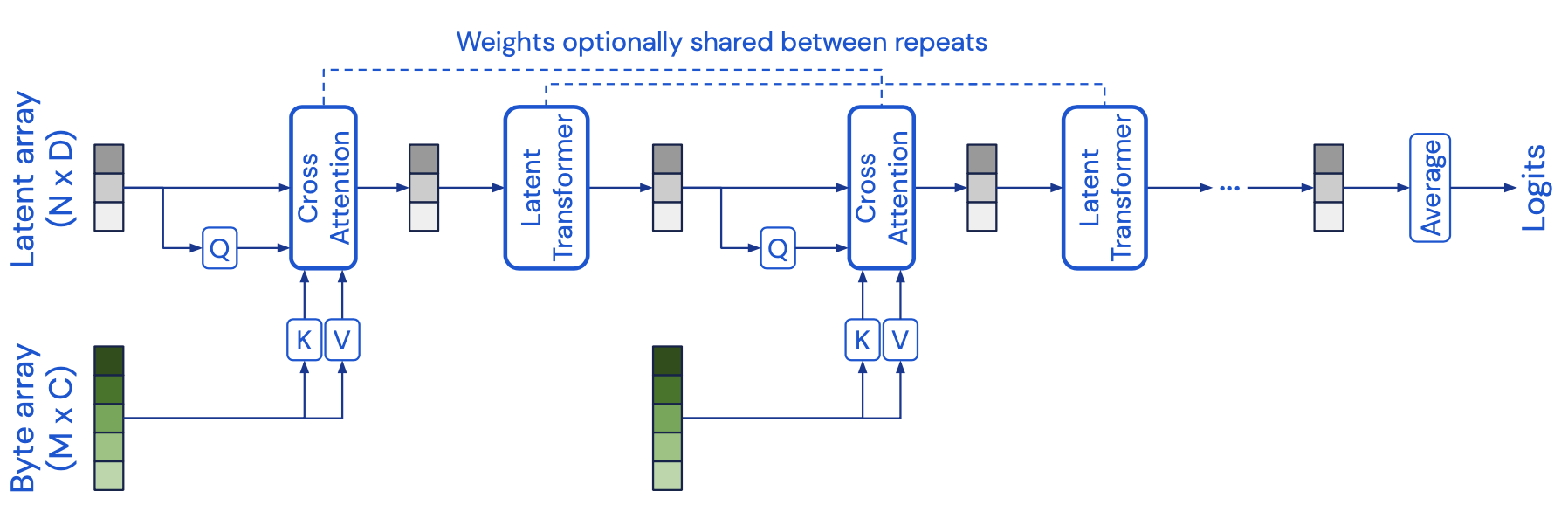
• Architecture
  • Cross attention module - maps a byte array and a latent array to a latent array
    • A byte array can be something like a pixel array etc.. (the input)
      • Generally large size \(M\)
    • Size of latent array is typically much smaller, and is a hyperparameter - size \(N\)
    • So, \(M << N\).
  • Transformer tower maps a latent array to a latent array
  • In essence, the cross-attention module projects a high-dimensional input byte array to a fixed-dimensional latent bottleneck
    • Then processes it using a deep stack of Transformer-style self-attention blocks in the latent space
  • Cross attention and the Transformer are applied in alternation
    • Allows Perceiver to iteratively attend to input byte array by alternating between cross attention and the latent self-attention blocks.
  • Asymmetric attention
    • Authors use the query-key-value (QKV) attention
      • Problem with QKV in Transformers is quadratic self-attention in input dimensionality
        • In standard QKV attention, \(Q \in \mathbb{R}^{M \times D}, K \in \mathbb{R}^{M \times C}, \text{ and } V \in \mathbb{R}^{M \times C}\) where \(C\) and \(D\) are channel dimensions and \(M\) is the input size.
        • So \(softmax(QK^T)V\) is \(\mathcal{O}(M^2)\)
      • Introduce assymmetry
        • \(Q\) is a projection of the learned latent array with index dimension \(N << M\), where \(N\) is a hyperparameter.
        • \(K\) and \(V\) are projections of the inputer byte array
        • Resulting cross attention operation is \(\mathcal{O}(MN)\)
  • Cross attention module takes the shape of input \(Q\)
    • Induces a bottleneck
    • which the authors exploit by building deep Transformers in the latent space - low cost of \(\mathcal{O}(N^2)\).
    • Hence latent Transformer has complexiity \(\mathcal{O}(LN^2)\), when considered as a function of the number of layers.
      • notice that a standard Transformer would be \(\mathcal{O}(LM^2)\)
  • Overall architecture - \(\mathcal{O}(MN + LN^2)\)
    • Input size (\(M\)) and depth (\(L\)) are decoupled
      • Allows construction of very large networks on large-scale data
  • Latent transformer uses GPT-2 architecture
    • based on the decoder of the orginal Transformer
  • Iterative cross-attention
    • Severity of the bottleneck may restrict the network’s ability to capture all of the necessary details from the input signal
      • Hedge against this by adding multiple cross-attend layers
        • Allows latent array to iteratively extract information
• Position encodings
  • Permutation invariance and position information
    • Attention is a permutation-invariant operation which is preserved by the Perceiver model.
    • However permutation invariance does not allow exploitation of spatial relationships in the input data.
    • Hence, they also include position encodings
  • Scalable Fourier Features
    • Authors use a parameterization of Fourier features
      • allows direct representation of the position structure of the input data
      • allows control over the number of frequency bands in the position encoding indepdently of the cutoff frequency
      • uniformly sample all frequencies up to a target resolution.
      • Frequency parametrized to take the values \([\sin(f_k\pix_d), \cos(f_k\pix_d)]\),
        • where \(f_k\) is the \(k^{th}\) band of a bank of frequencies spaced equally between 1 and \(\frac{\mu}{2}\). \(\frac{\mu}{2}\) can be naturally interpreted as the Nyquist frequency, where \(\mu\) is the target sampling rate.
        • \(x_d\) is the value of input position along the \(d^{th}\) dimension - for images \(d = 2\). \(x_d \in [-1, 1]\).
      • related to the NeRF position encoding scheme (Mildenhall et al., 2020).
  • Position encodings are generally applicable.
    • Feature based approach allows the network to learn how to use (or ignore) the position structure
    • Position encoding can be easily adapted to a new domain as Fourier features are trivial to adapt as long as the input dimension is relatively small and known
    • Position encodings can be extended to multimodal data - each domain has it’s own position encoding.

How well does the paper perform?

• Pretty competitively with other models
• 
  • Top-1 validation accuracy (in %). Compares baseline from literature, baseline with Fourier Features, Transformer with Fourier Features against Perceiver. Perceiver performs as well as baseline.
• 
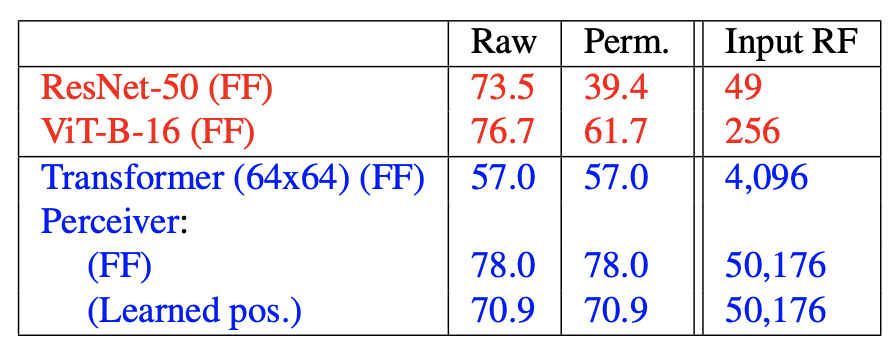
  • Top-1 validation accuracy (in %). Shows the Perceiver model’s resiliency to permuted dataset. This is due to global attention. Input RF refers to the Input Receptive Field (RF) in pixels - this is the size of the local neighbourhood used for 2D convolutions
• 
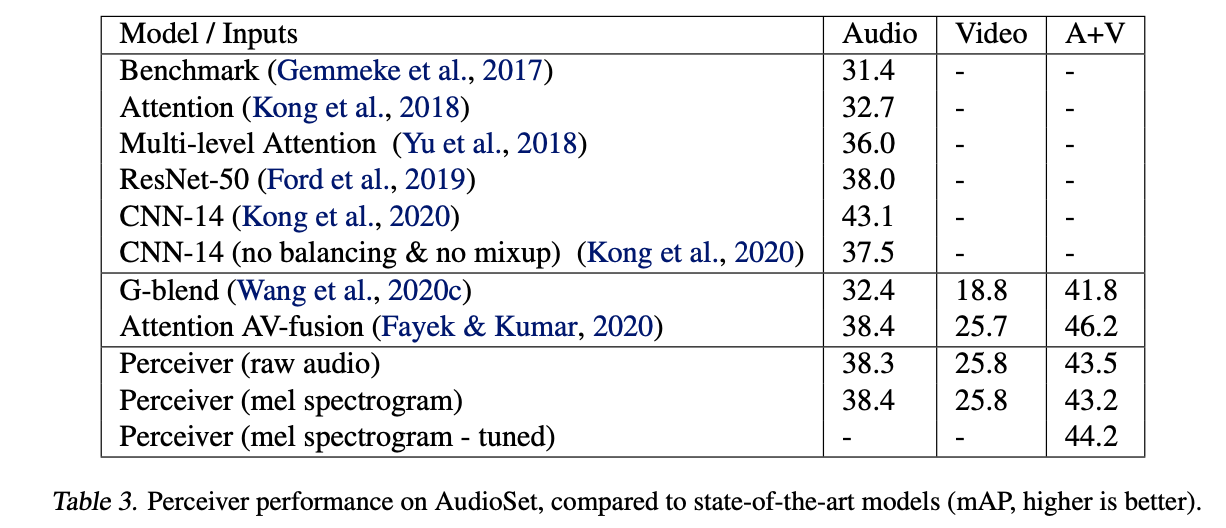
  • Very comparable results. In future work, hope to incorporate the insights that are also used in CNN-14 (Kong et al., 2020).
• 
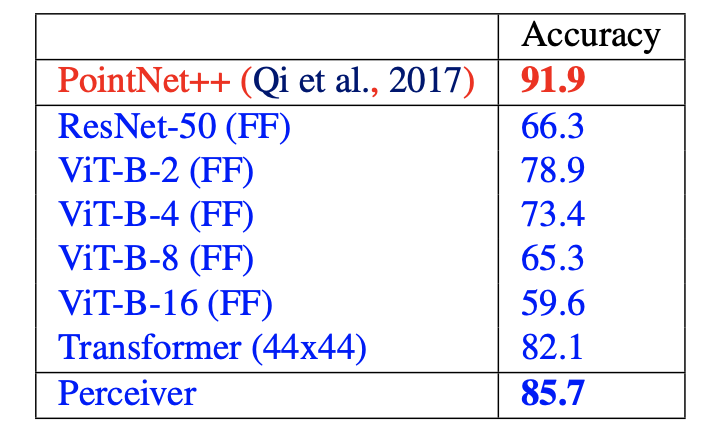
  • Top-1 validation accuracy (in %) on Model-Net40. PointNet++ uses extra geometric features and other techniques not used in the blue models.

TL;DR

• Uses iterative asymmetric cross-attention to decouple network depth from input size allowing for large networks
• Motivated to be a generalisable architecture - and thus, Is a multimodal architecture
• Performs competitively against specialised models with inductive biases baked in.