Implicit Geometric Regularization for Learning Shapes, Gropp, Yariv, Haim, Atzmon, Lipman; 2020 - Summary
| author: | mmcinnestaylor |
| score: | 8 / 10 |
Core idea?
- 2D and 3D Shapes can be represented as level sets of neural networks.
- Neural shape representations can be learned from raw data by using implicit geometric regularization.
- Implicit neural representations can be achieved without 3D supervision and/or a direct loss on the zero level set.
Technical Implementation
- Given: a point cloud \(X = \{x_i\}_{i\in I}\subset\mathbb{R}^3\) with or without normal data \(N =\{n_i\}_{i\in I}\subset\mathbb{R}^3\)
- Goal: compute the parameters \(\theta\) of a Multilayer Perceptron(MLP) \(f(x;\theta)\) where \(f:\mathbb{R}^3\times\mathbb{R}^m\rightarrow\mathbb{R}\) so that it approximates a signed distance function to a surface \(M\) defined by \(X\text{ and }N\).
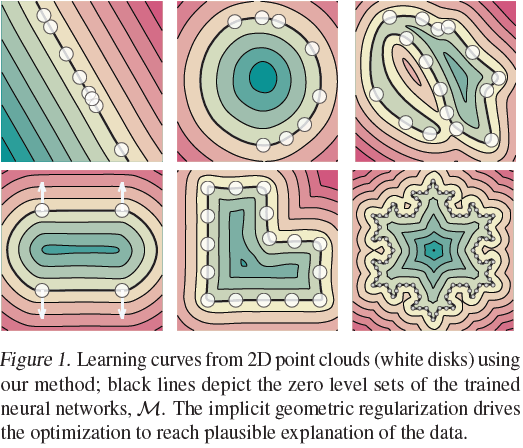
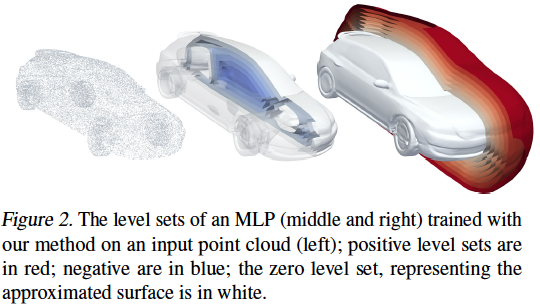
- Using loss: \(l(\theta) = l_x(\theta) + \lambda\mathbb{E}_x(\Vert\nabla_xf(x;\theta)\Vert-1)^2\)
- Note: \(\lambda>0\) is a parameter, \(\Vert\cdot\Vert=\Vert\cdot\Vert_2\) is the euclidean 2-norm
- The authors prove this funciton has the plane reproduction property: if the point cloud \(X\) is sampled approximately from a plane \(H\), then gradient descent on the loss converges to the approximate signed distance function to \(H\).
- The first term: \(l_x(\theta)=\frac{1}{I}\sum_{i\in I}(\lvert f(x_i;\theta)\rvert+\tau\Vert\nabla_xf(x_i;\theta)-n_i\Vert)\)
- encourages \(f\) to vanish on \(X\) and if normal data exists, that \(\nabla_xf\) is close to the normals \(N\)
- The second term is the Eikonal term, and encourages \(\nabla_xf\) to be of unit 2-norm
- A solution to the Eikonal PDE has the form \(\Vert\nabla_xf(x)\Vert=1\)
- A solution for point boundary data \(X, N\) is not unique
- Furthermore a solution will be a signed distance function and a global minimum of of the loss equation
- The expectration is taken w.r.t. some probability distribution in \(\mathbb{R}^3\)
- A solution to the Eikonal PDE has the form \(\Vert\nabla_xf(x)\Vert=1\)
- Optimization uses Stochastic Gradient Descent
- Architecture:
- 8 layers each with 512 hidden units
- single skip connection from the input to the middle hidden layer
- weights \(\theta\in\mathbb{R}^m\) initialized using geometric initialization
- loss parameters \(\lambda=0.1, \tau=1\)
- Distribution:
- distribution of the expectation \(\mathbb{E}\) is the average of a uniform distribution and a sum of Gaussians centered at \(X\)
- standard deviation equal to the distance to the k-th nearest neighbor (k=50)
- Level set extraction:
- utilizes the Marching Cubes meshing algorithm on uniform samples grids of size \(l^3\), \(l\in\{256,512\}\)}
- Evaulation metrics:
- calculating the Chamfer and Hausdorff distances on point sets \(X_1,X_2\subset\mathbb{R}^3\)
- Chamfer: \(d_C(X_1,X_2)=\frac{1}{2}(d_{\overrightarrow{C}}(X_1,X_2)+d_{\overrightarrow{C}}(X_2,X_1))\)
- where: \(d_{\overrightarrow{C}}(X_1,X_2)=\frac{1}{\lvert X_1\rvert}\sum_{x_1\in X_1}\text{min}_{x_2\in X_2}\Vert x_1-x_2\Vert\)
- Hausdorff: \(d_H(X_1,X_2)=\text{max}\{d_{\overrightarrow{H}}(X_1,X_2),d_{\overrightarrow{H}}(X_2,X_1)\}\)
- where: \(d_{\overrightarrow{H}}(X_1,X_2)=\text{max}_{x_1\in X_1}\text{min}_{x_2\in X_2}\Vert x_1-x_2\Vert\)
Variants
The model’s architecture was extended to learn multiple shapes.
- The MLP is thus defined as \(f(x;\theta;z_j)\)
- Where \(z_j\in\mathbb{R}^{256}\) is a latent vector corresponding to each training example \(j\in J\)
- Latent vectors are initialized to \(0\in\mathbb{R}^{256}\)
- The loss takes the form of \(\frac{1}{\lvert B\rvert}\sum_{j\in B}l(\theta,z_j)+\alpha\Vert z_j\Vert\)
- Where \(B\subset J\) is a batch, \(\alpha=0.01\), and \(l,\tau,\lambda\) are as defined above.
Results
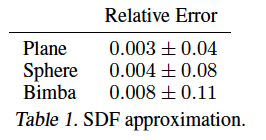
Signed Distance Function Approximation
MLPs trained independently on 3 different shapes.

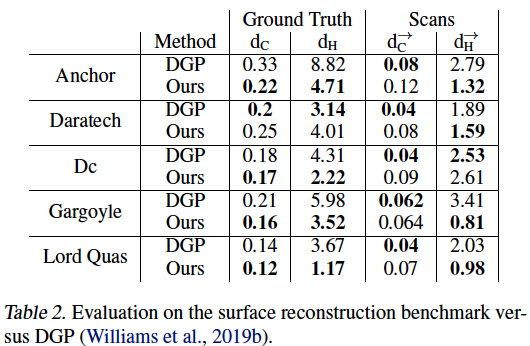
Surface Reconstruction
The paper’s method outperformed DGP on 4 out of 5 tasks.
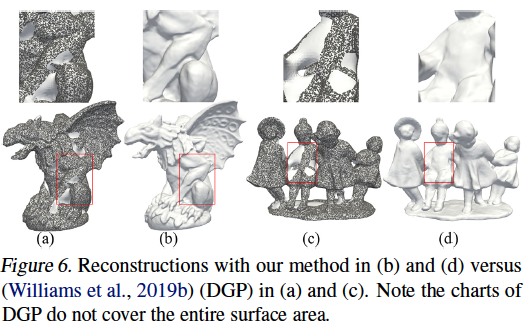
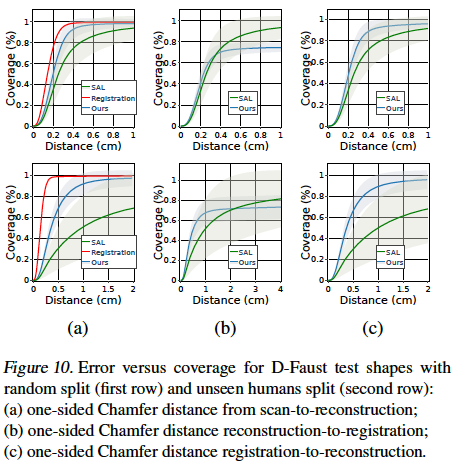
Learning Shape Space
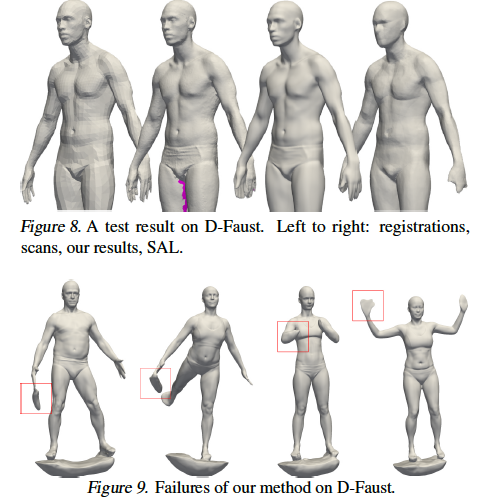
The authors noted that their model was sensitive to noisy normal data, as seen in Figure 9.
TL;DR
- High fidelity implicit neural representations of shapes can be learned directly from raw data using a simple loss function
- Optimization using gradient descent tends to find a favorable minima out of the infinite possible signed distance functions
- This method’s primary shortcoming is sensitivity to noisy normals