| author: | ywen666 |
| score: | 9 / 10 |
Background:
Same authors as the last paper. The last paper studied the weight initialization and mentioned that neither sigmoid and tanh is a good activation function. So naturally they studied what could be a good alternative activation function.
The core idea:
Neuroscience observations suggest that our neurons encode information in a highly sparse fashion. However without explicit L1 regularization, deep neural networks are not designed to honor sparsity.
For example, a commonly used non-linear activation function sigmoid has a stead state at 1/2, which means neurons tend to fire at half their saturation regime (this is dense represenations).
Even from the view of machine learning researchers, sparsity is a concept of interest. A dense representation is highly entangled because almost any change in the input modifies most of the entries in the representation vector. This violates the postulation that deep learning algorithms disentangle the factors which can explain the variations in the data.
Therefore, this paper propose to explore the use of rectifying non-linear activation functions as alternatives to the hyperbolic tangent or sigmoid in deep artificial neural networks to promote sparsity.
Advantages of rectifier(x) = max(0, x) as activation functions
- It naturaly induces 50% inactive neurons, leading to desirable sparsity.
- When neurons are active, they are linear. This allows gradient signals to backprop without any loss of information.
- The computation is efficient and the implementation is easy.
Potential problems:
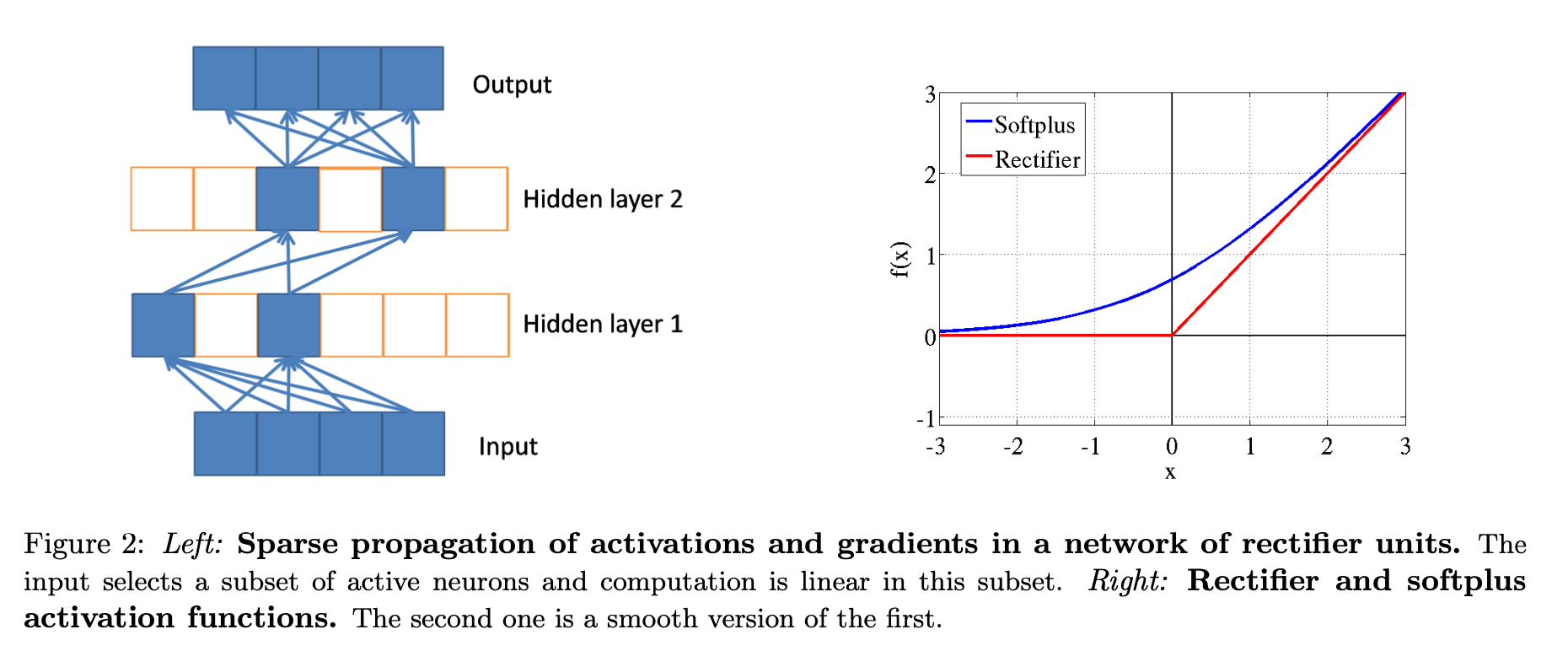
It is non-differentiable at 0. A variant – softplus $f(x) = log(1 + e^x)$ was also proposed. The figure illstruates the difference between ReLU and Softplus.
Experiments
Experiements in this paper cover image recognition (MNIST, CIFAR10, NISTP and NORB) and sentiment analysis (opentable review data).
Experiments on both image and text data indicate that training proceeds better when neurons are either off or operating mostly in a linear regime. This justifies the use of rectifying non-linear activation functions.
Moreover, ReLU performed better than other commonly used activation functions such as tanh and sigmoid, especially without unsupervied pretraining.
The hard threshold at 0 does not lead to any optimization issue as the authors observed that ReLU and softplus reached similar performance.
Rectifier networks are deep sparse networks. There is an average exact sparsity (fraction of zeros) of the hidden layers of 83.4% on MNIST, 72.0% on CIFAR10, 68.0% on NISTP and 73.8% on NORB. Additional experiments with L1 regularization showed that sparsity under 85% will not hurt model accuracy.
TL;DR
Sparsity is important in both views of neurosciencists and machine learning researchers. This paper proposed an alternative non-linear activation function – ReLU to promote sparsity in deep neural networks.