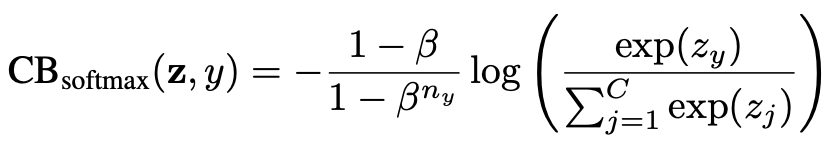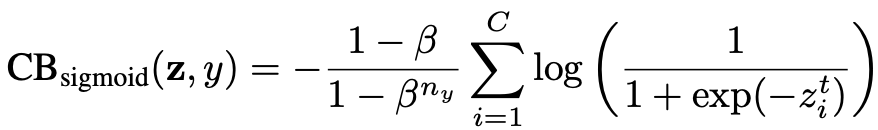| author: | ishank-arora |
| score: | 9 / 10 |
What is the core idea?
With large-scale data comes the problem of having only a few classes account for most of the data, while most other classes being under-represented.
Therefore, it is critical to address the problem of tailed data distribution.
In this paper, the authors design a re-weighting scheme that uses the effective number of samples for each class to re-balance the loss.
The key idea is to associate each sample with a small neighboring region instead of a single point.
How is it realized (technically)?
The effective number of samples is defined simply as:
\[E_n = \frac{(1-\beta^n)}{(1-\beta)}\]where \(n\) is the number of samples and \(\beta \in [0,1)]\) is a hyperparameter.
Consider the data sampling process as a simplified version of random covering
- Given a class, let’s call the set of all possibe data in the feature space of this class as \(\mathbf{S}\).
- We assume the volume of \(\mathbf{S}\) is \(N\) and \(N \ge 1\).
- Randomly sampling from \(\mathbf{S}\) as a way to sample data and considering it as a random covering problem implies that the when more data is sampled, the coverage of \(\mathbf{S}\) is better.
- The expected total volume of sampled data increases as the number of data increases, and is bounded by \(N\).
- Calculating expected total volume is a difficult problem
- The authors simplfied the problem such that partial covering is not considered
- Hence, newly sampled data can only interact with the previously sampeld data by either being inside the set of previously sampled data (with probability \(p\)) or not. See figure 2
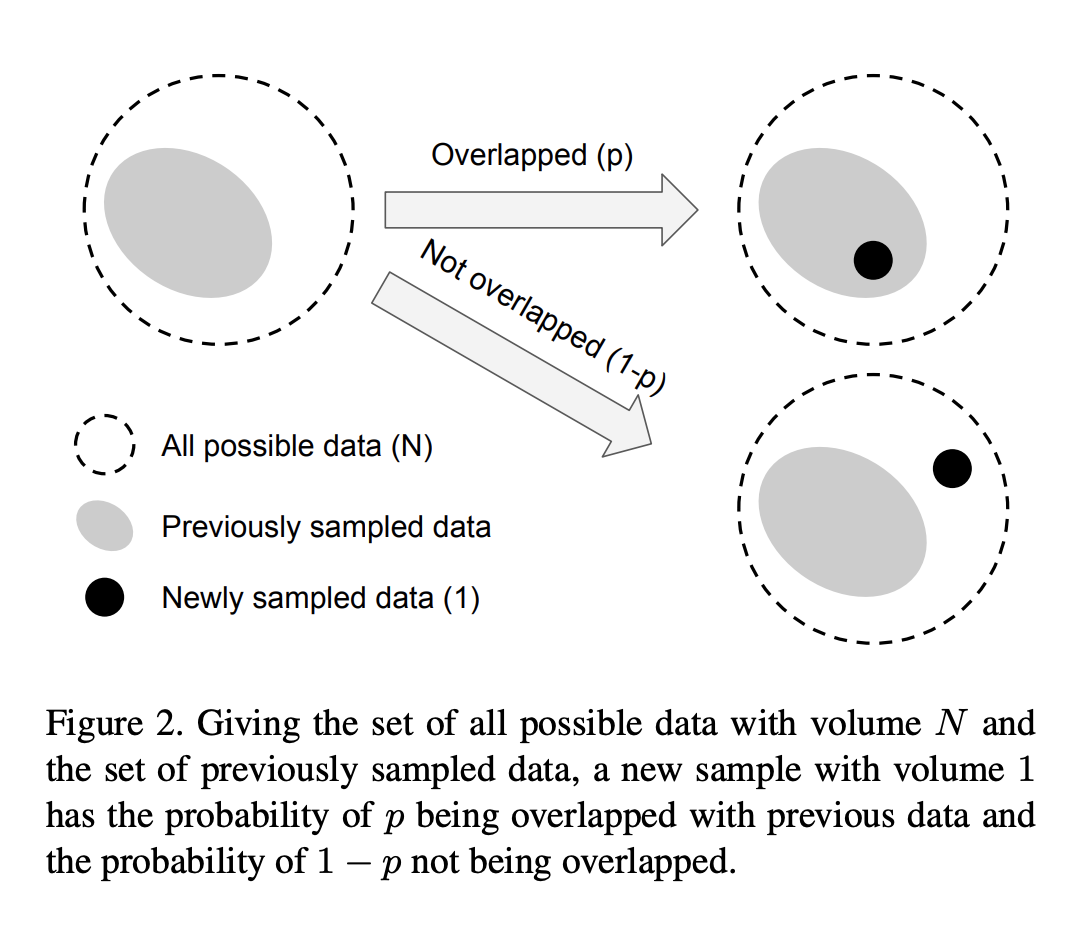
- With \(\beta = \frac{N-1}{N}\), the formula \(E_n\) holds through proof by induction.
The idea of the authors is to capture the diminishing marginal benfits by using more data points of a class.
- Highly likely, due to intrinsic similarities, that in real-world data, a newly added sample is a near-duplicate of existing samples.
CNNs are trained with heavy data augmentations (random cropping, re-scaling, horizontal flipping)
- Small neighboring region of a sample able to caputre all near-duplicates that can be obtained by data augmentation.
- Hence, a large \(N\) means the effective number of samples for a class is the same as the number of samples \(n\), so no data overlap
- On the other hand, a small \(N\), \(N=1\) means that there exists a single prototype that can represent all data in a class via data augmentation.
Class-Balanced Loss
Addresses the problem of training imbalanced data by introducing a weighting factor inversely proportional to \(E_n\).
The following loss functions are described in the paper.
- Class-Balanced Softmax Cross-Entropy Loss
- Class-Balanced Sigmoid Cross-Entropy Loss
- Class-Balanced Focal Loss
- Focal Loss adds a modulating factor to the sigmoid CE loss
- This allows the model to focus on difficult samples, instead of well-classified samples
- Introducing a class-balanced version of Focal Loss will therefore be interesting to compare as both losses are trying to solve the problem introduced by class imbalance in the data.
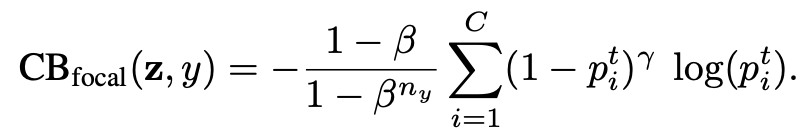
- Focal Loss adds a modulating factor to the sigmoid CE loss
How well does the paper perform?
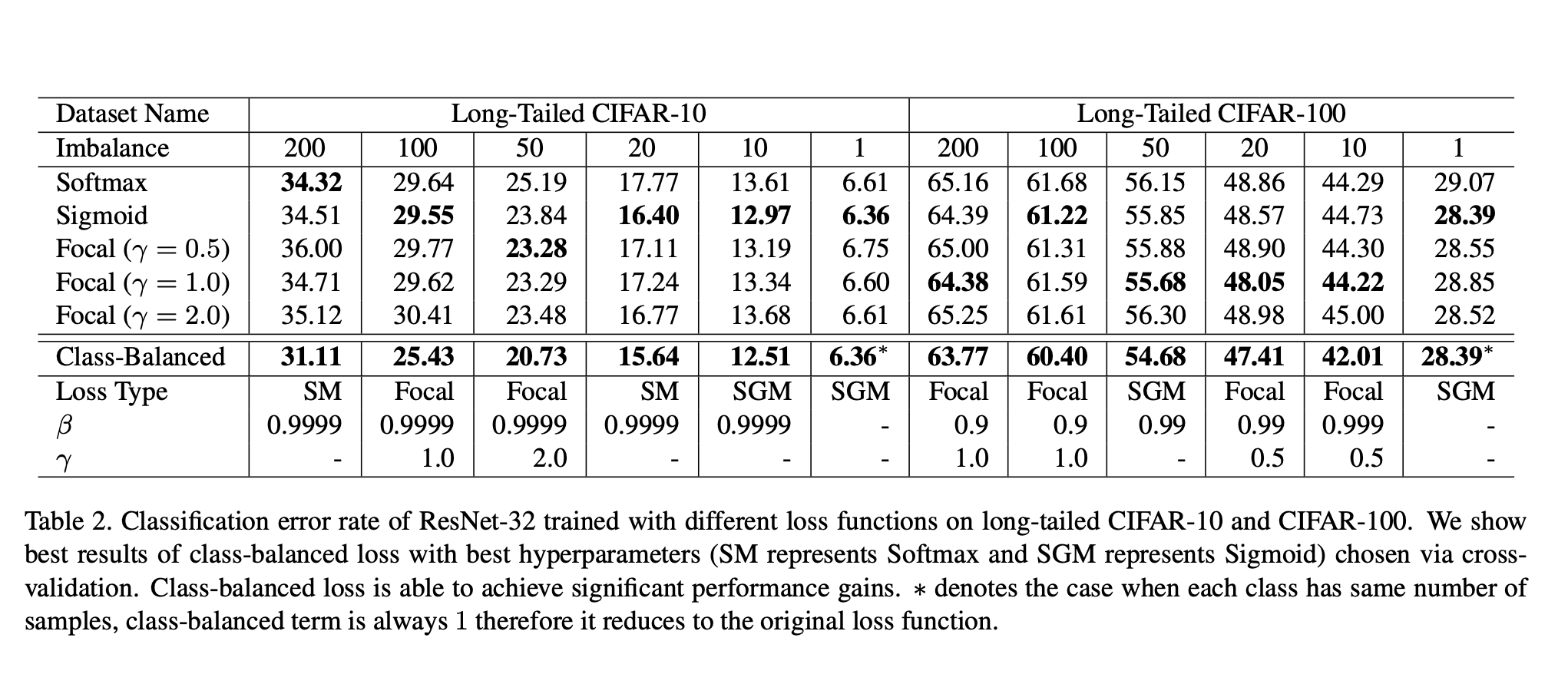
- Notice how the class-balanced losses, even when compared to normal Focal Loss, is the most optimal
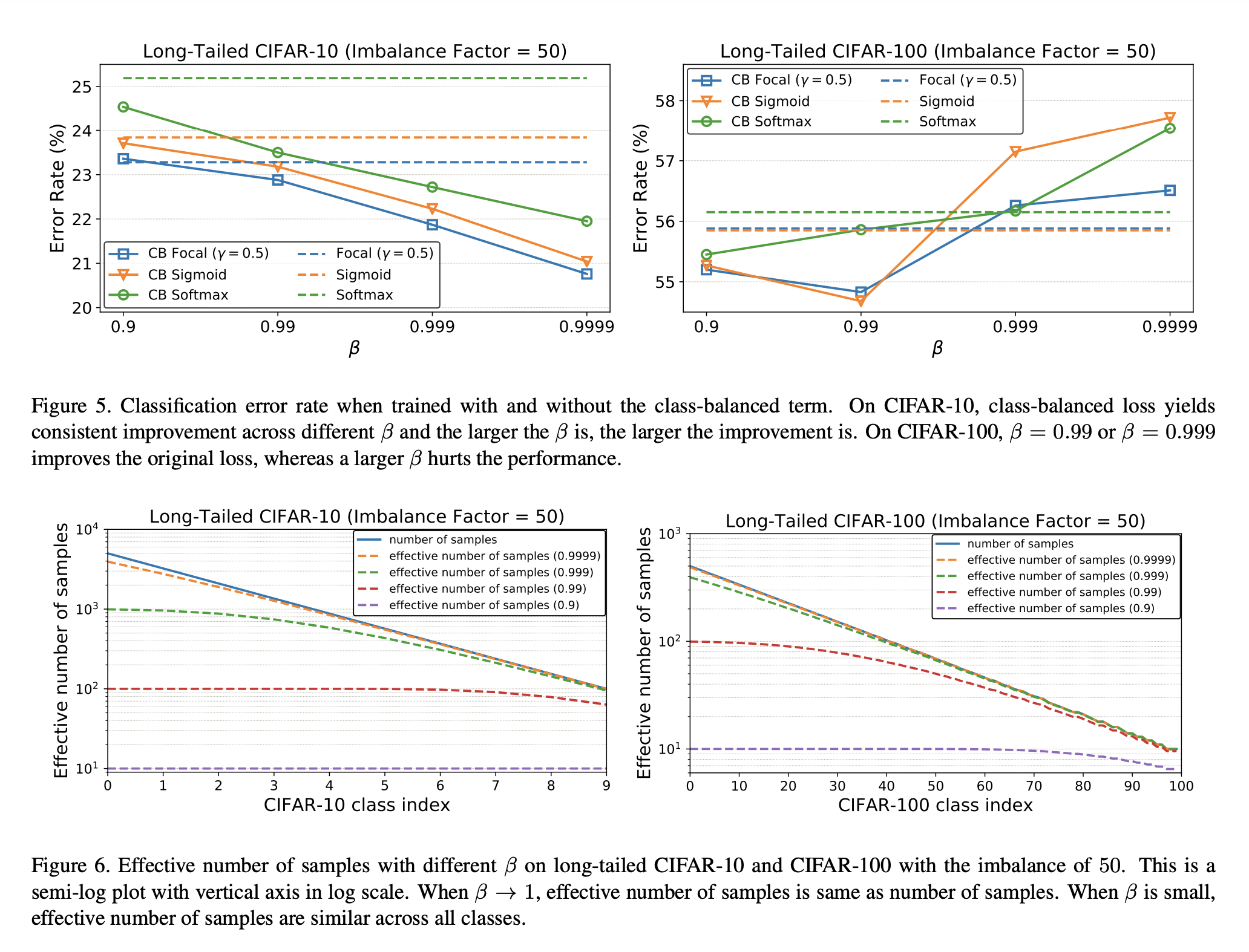
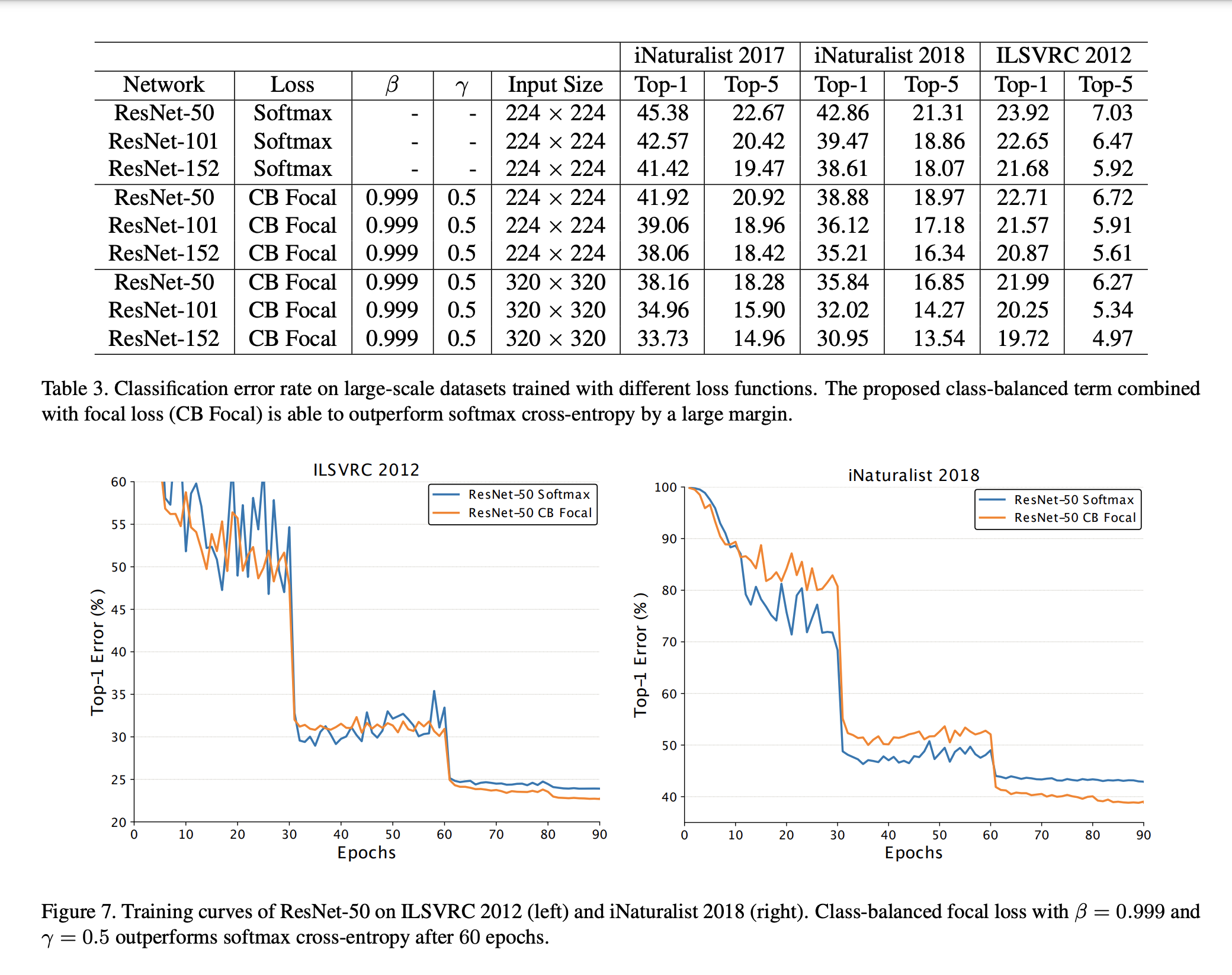
TL;DR
- Accounting for class imbalance in the training data by using class-balanced loss functions gives the best loss values
- Using the effiective number of samples \(E_n\) for some class, softmax cross entropy, sigmoid cross entropy, and focal loss can be applied in a class-balanced fashion.
- The effective number of samples is defined as \(E_n = \frac{(1-\beta^n)}{(1-\beta)}\)