| author: | rll2396 |
| score: | 7 / 10 |
TODO: Summarize the paper:
- What is the core idea?
- Sequential data often has long-term dependencies
- RNNs have trouble capturing these dependencies due to vanishing/exploding gradients
- The LSTM and GRU activation functions have been proposed to address this issue
- In this paper, the author compare how these functions perform empirically
- How is it realized (technically)?
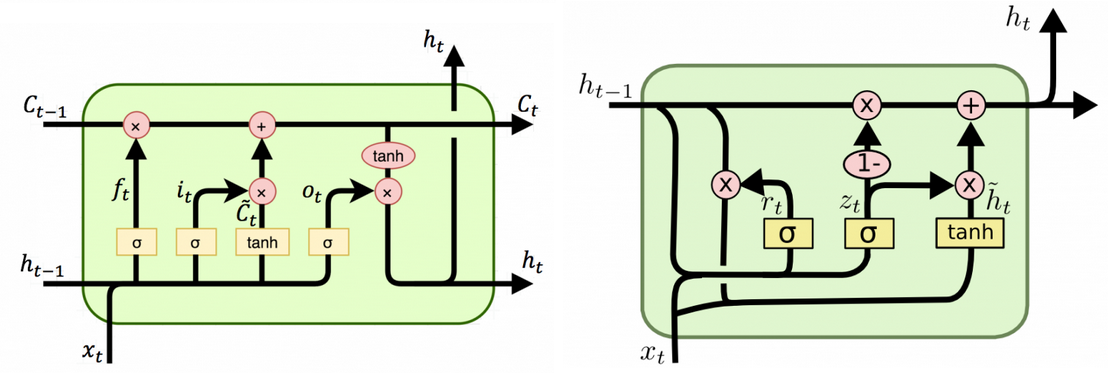
- LSTM
-
\(\textbf{x}_t\) and \(\textbf{h}_{t-1}\) are used to calculate the forget gate, the input gate, and the output gate
\[f_t = \sigma(W_f\textbf{x}_t + U_f\textbf{h}_{t-1})\] \[i_t = \sigma(W_i\textbf{x}_t + U_i\textbf{h}_{t-1})\] \[o_t = \sigma(W_o\textbf{x}_t + U_o\textbf{h}_{t-1})\] -
Candidate memory cell calculated as
\[\tilde{c}_t = \tanh(W_c\textbf{x}_t + U_c\textbf{h}_{t-1})\] -
New memory cell calculated by “forgetting” some of the old memory and “inputting” some of the candidate memory according to the forget and input gates
\[c_t = f_tc_{t-1} + i_t\tilde{c}_t\] -
Finally, the output hidden state is calculated as
\[h_t = o_t\tanh(c_t)\]
-
- GRU
-
\(\textbf{x}_t\) and \(\textbf{h}_{t-1}\) are used to calculate the reset and update gates
\[r_t = \sigma(W_r\textbf{x}_t + U_r\textbf{h}_{t-1})\] \[z_t = \sigma(W_z\textbf{x}_t + U_z\textbf{h}_{t-1})\] -
Candidate activation is calculated as
\[\tilde{h}_t = \tanh(W\textbf{x}_t + U(\textbf{r}_t \odot \textbf{h}_{t-1}))\]where \(\odot\) is elementwise multiplication
-
Finally, the new activation is calculated as an interpolation between the old activation and the candidate activation
\[h_t = (1-z_t)h_{t-1} + z_t\tilde{h}_t\]
-
- Clear similiarity between the two is that some memory is kept with some new memory added on top
- Tradition recurrent units completely replace old memory
- This helps the model remember features that occurred several time steps before
- Also provides shortcuts for the gradient to propagate through
- LSTM can control output \(h_t\) through output gate
- GRU can directly control how much of \(h_{t-1}\) to use to calculate the new \(h_t\)
- For GRU, one gate controls how much previous and candidate memory is used to calculate the new memory
- For LSTM, independent gates control previous and candiate memory
- LSTM
- How well does the paper perform?
- The LSTM and GRU are evaluated on the task of sequence modeling, along with tanh as a benchmark
- They are tested on three music datasets and two Ubisoft speech datasets
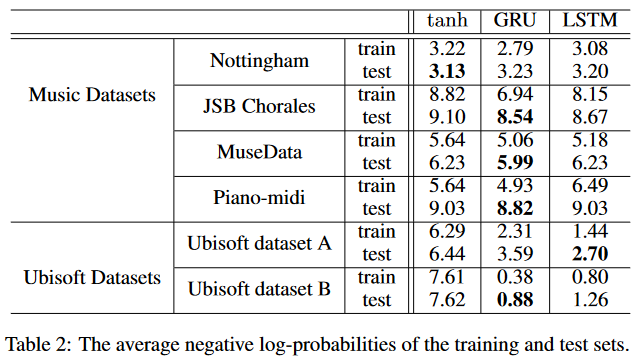
- For the music datasets, all three perform comparably, with GRU performing the best most of the time
- For the speech datasets, LSTM and GRU perform way better than tanh
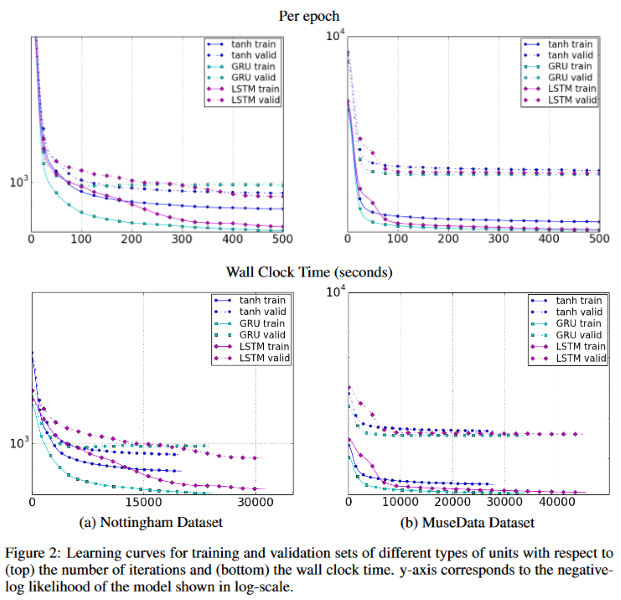
- For the music datasets, the three types again all perform comparably, with GRU having a slight edge in terms of convergence rate
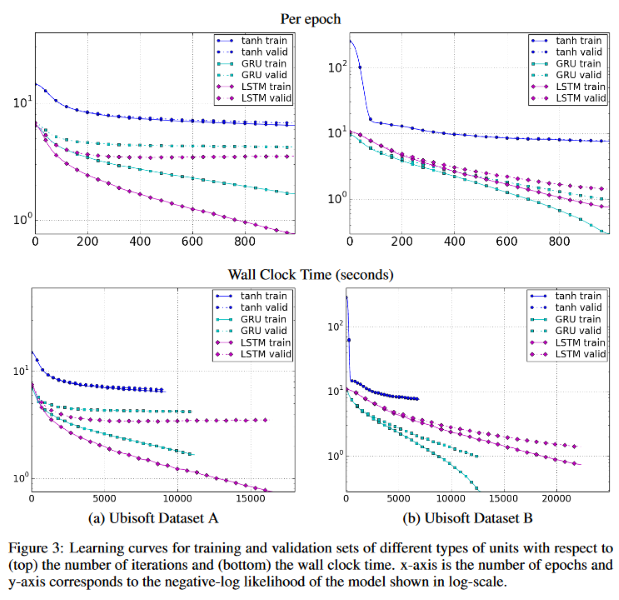
-
For the speech datasets, tanh converges at a much worse performance than the other two
-
Overall, LSTM and GRU are clearly better than tanh, yet results for which of the two is better are mixed
TL;DR
- RNNs suffer from vanishing/exploding gradients
- LSTM and GRU, which are more sophisticated activation functions, can mitigate this problem
- Empirically shown that neither function has a distinct advantage over the other