Generating Long Sequences with Sparse Transformers, Child, Gray, Radford, Sutskever; 2019 - Summary
| author: | ishank-arora |
| score: | 9 / 10 |
- What is the core idea?
- This paper introduces Spare Transformers.
- Sparse transformers are a variation on Transformers
- Sparse Transformers introduce sparse factorizations of the attention matrix which reduces the time and memory required by transformers from \(O(n^2)\) to \(O(n\sqrt{n})\).
- The paper also introduces
- A variation of the Transformer architecture and initialisation for training Sparse Transformers on even deeper networks
- Recomputing attention matrices
- Fast attention kernels for training
- Background
- Let’s consider the task of autoregressive sequence generation
- An autoregressive model predicts future behavour based on past behaviour
- The joint probability of a sequence \(\mathbf{x} = \{x_1, x_2, x_3, ..., x_n\}\) can be modeled as the product of conditional probability distributions and parameterized by a network \(\theta\).
- \[p(x) = \prod_{i=1}^{n} p(x_i \mid x_1, ..., x_{i-1};\theta)\]
- The network \(\theta\) takes in the sequence of tokens and outputs a categorical distrubition using softmax over a vocabulary of size \(v\).
- \(\theta\) is typicall a Transformer in decode-only mode.
- The self-attention portion computes \(n\) weightings for each of the \(n\) elements.
- This is intractable as the sequence length grows
- Let’s consider the task of autoregressive sequence generation
- How is it realized (technically)?
- Factorized Self-Attention
- First, the authors visualised the attention patterns learned by a 128-layer self-attention network on CIFAR-10.
- The authors noticed that most layers had sparse attention patterns in most data points
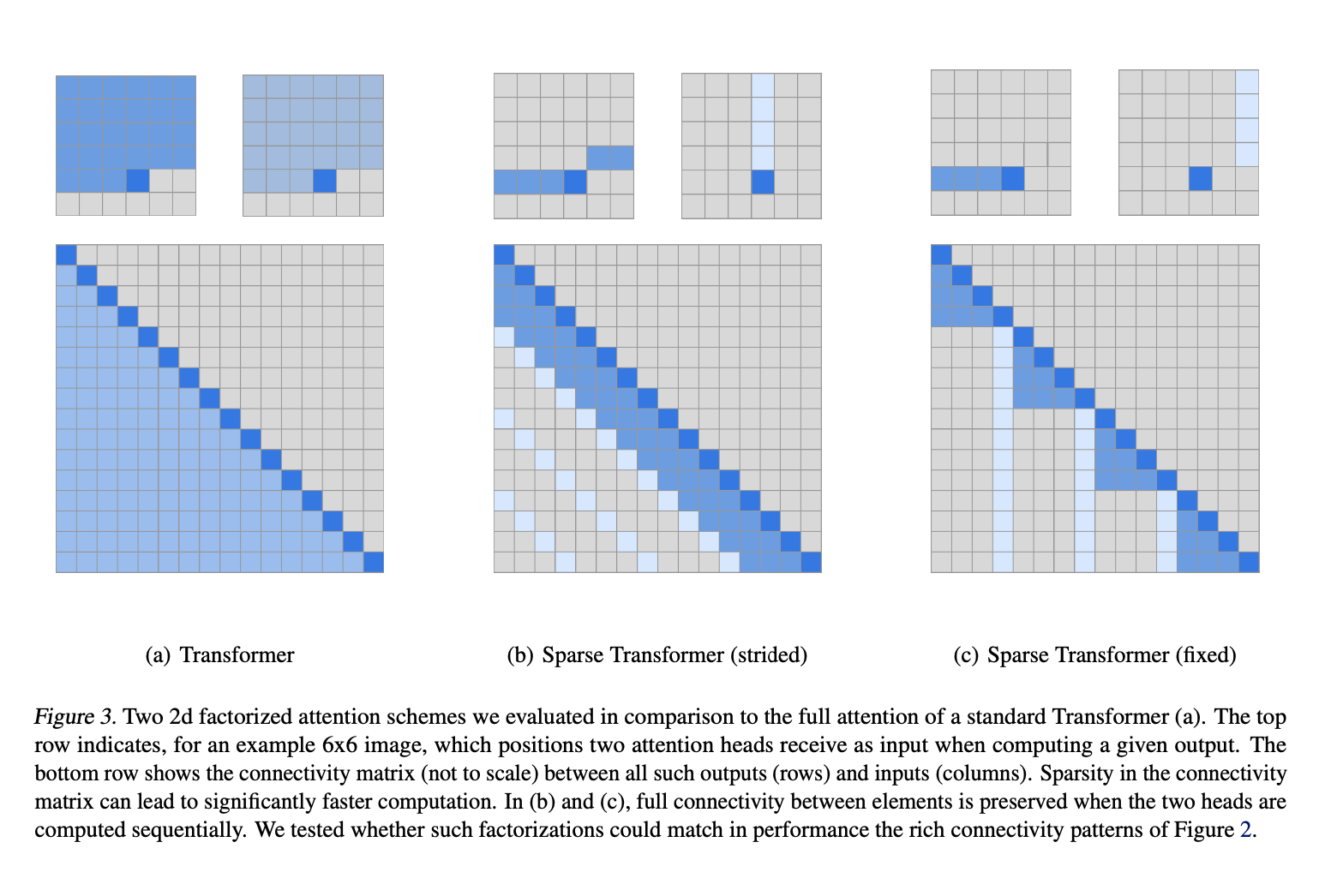
- This suggests that some form of sparsity can be introduced without significantly affecting performance.
- This lead to Factorized Self Attention
- Full self-attention for autoregressive models allows every element to attend to all previous positions and its own position
- Factorized self-attention, on the other hand, has \(p\) separate attention heads
- The \(m\)th head defines a subset of the indices \(A_i^{(m)} \subset \{j : j \le i\}\). This subset of indices is what the \(m\)th head attends to.
- \(A_i^{(m)}\) is chosen effienctly i.e. \(\text{cardinality}(A_i^{(m)}) \propto \sqrt[p]{n}\)
- In this paper - \(p=2\)
- One head attends to previous \(l\) locations
- The other head attends to every \(l\)th location, where \(l\) is the stride and chosen to be close to \(\sqrt{n}\)
- This is referred to as strided attention
- Works well for data that has a structure which aligns with the stride - like images or some types of music
- Does not work well for text
- For text, the paper uses \(\textit{fixed}\) attention.
- Here specific cells summarize previous locations and propogate that informatino to all future cells
- Factorized self-attention, on the other hand, has \(p\) separate attention heads
- First, the authors visualised the attention patterns learned by a 128-layer self-attention network on CIFAR-10.
- Sparse Transformer
- Modified version of the Transformer
- Incorporates Factorized attention
- Three ways to do so
- One attention type per residual block, interleaved sequentially or at a ratio determined as a hyperparameter
- Merged head - a single head attends to locations of the pixels that both factorized heads would attend to
- Multi-head attention - attention produced are computed in parallel, then concatenated along the feature dimension
- Three ways to do so
- Scaling to hundreds of layers
- Transformers hard to train with many layers
- To tackle this, the following archtectural changes were adopted:
- Pre-activation of residual block definition from (He et al. 2016)
- Modeling diverse data types
- Learned embeddings which either encoded the structure of the data or the factorized attention patterns important for model’s success
- Saving memory by recomputing attention weights
- Gradient checkpointing is proven to be effective in reducing memory requirements (Chen et al. 2016) (Gruslys et al. 2016)
- This technique can also be applied to self-attention layers when long sequences are processed
- With recomputation alone, dense attention networks with hundreds of layers can be trained on sequence lengths of 16,384
- Infeasible on modern hardware otherwise
- Gradient checkpointing is proven to be effective in reducing memory requirements (Chen et al. 2016) (Gruslys et al. 2016)
- Efficient block-sparse attention kernels
- Attention can be efficiently computed
- The paper implemented a set of GPU kernels to do so
- Halved number of operation to be performed
- Attention can be efficiently computed
- Mixed precision Training
- Network weights computed in single precision floating point
- Network activations and gradients in half-precision
- Accelarates training
- Factorized Self-Attention
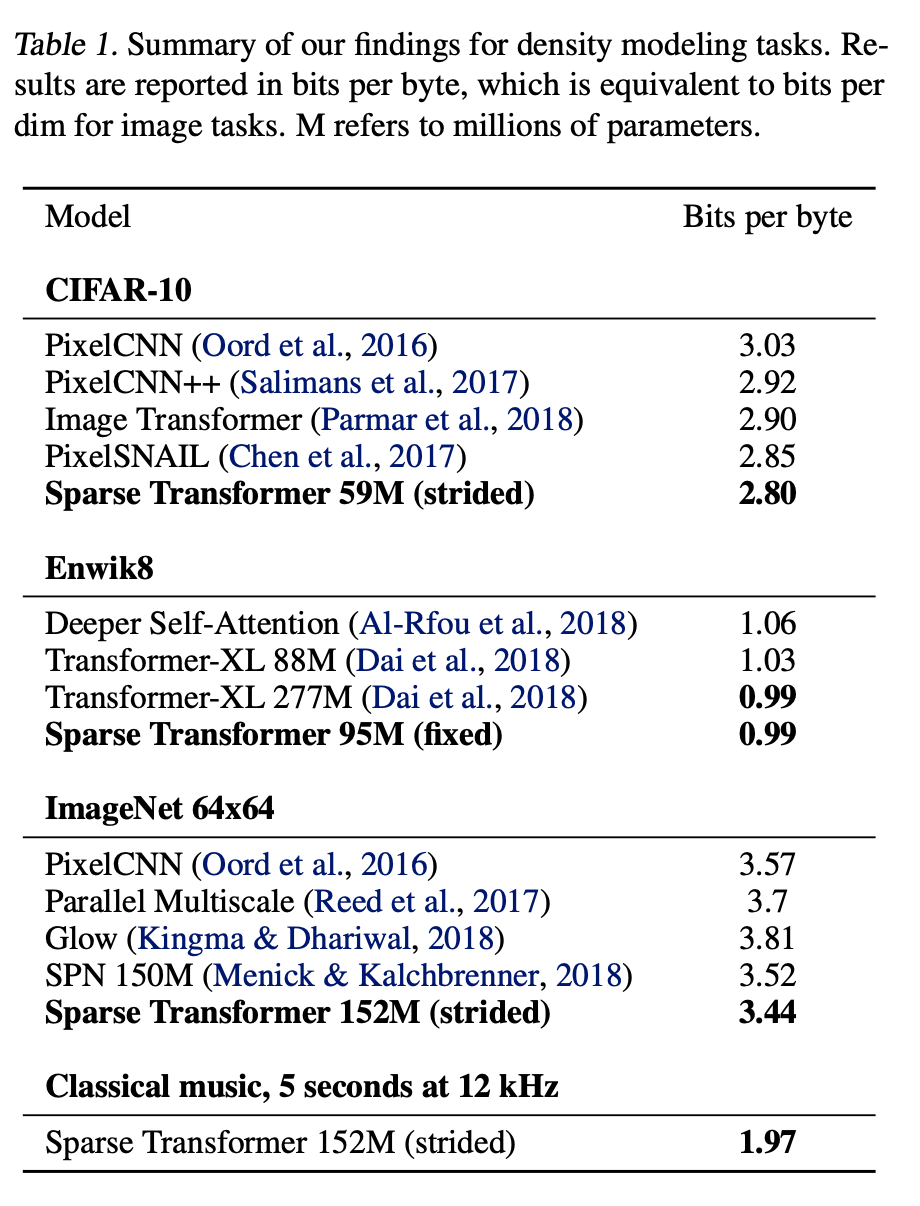
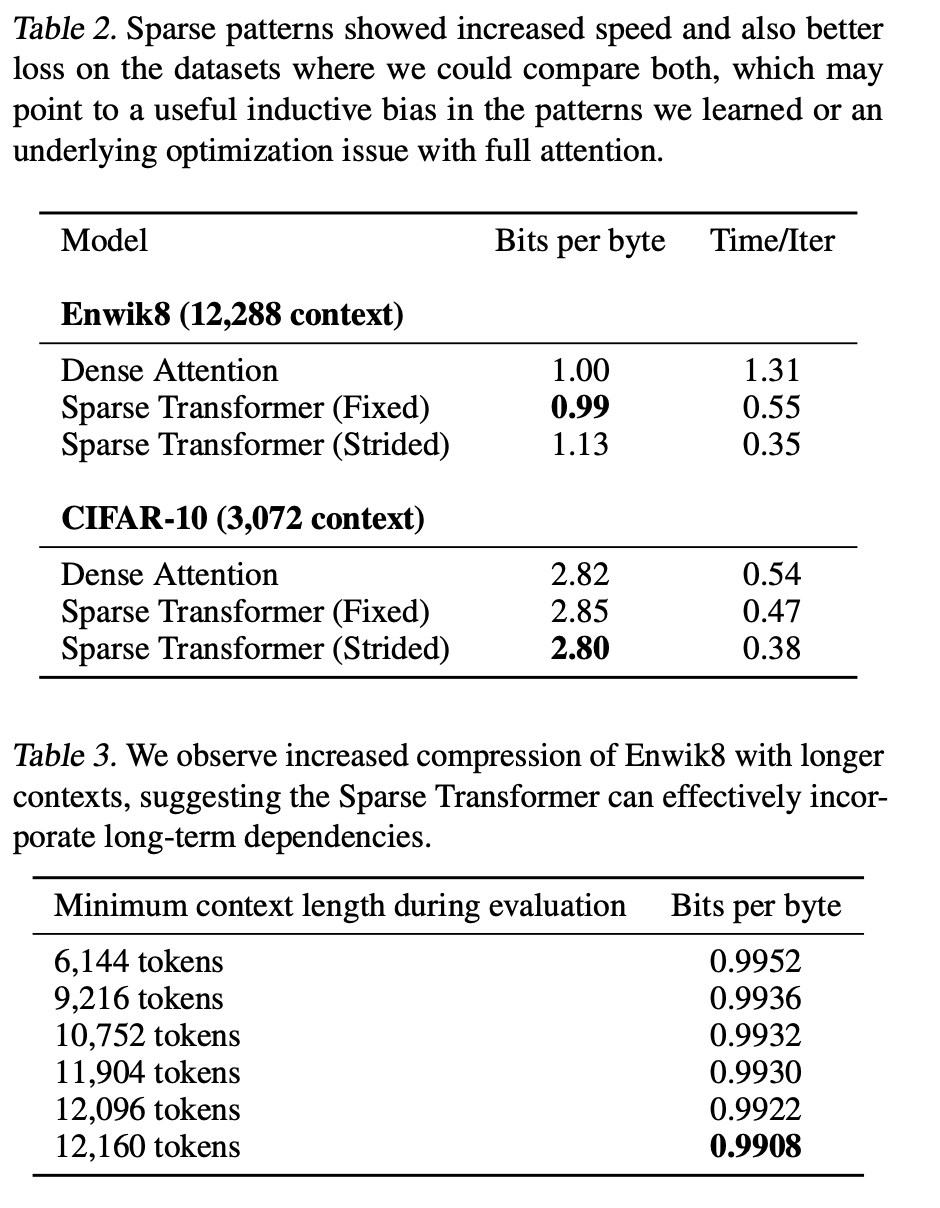
- How well does the paper perform?
-
Runs sigificantly faster than full attention
-
Converged to a lower error due to sparse patterns
- May be due to an underlying optimisation issue with full attention
- Or a useful inductive bias from introduced sparsity patterns
-
-
TL;DR
- Attention in most layers has a sparse pattern - recognising this led to the insight that full attention may not need to be computed, and instead, introducing sparsity in computing attention may help - this led to factorised self-attention
- Reduces computation costs and thus allows for training of deeper networks with longer sequences
- Equivalent or better results in accuracy while reducing computation time and memory.