Large-Scale Machine Learning with Stochastic Gradient Descent, Bottou; 2010 - Summary
author: zayne-sprague
score: 7 / 10

Main Idea

Stochastic Gradient Decent, although slower than Gradient Decent in optimization, it is able to reach a predefined expected risk in less time, making it better for large scale machine learning problems.

Gradient Decent vs Stochastic Gradient Decent

Gradient Decent will run the entire training data set before updating the weights.

Stochastic Gradient Decent will update the weights per randomly sampled training example.

How is it realized

How Stochastic Gradient Decent (SGD) works is fairly similar to Gradient Decent (it’s actually simpler)

Given a training set pair \(x\) and \(y\), and a parameterized function \(f_{w}(x)\) where \(w\) is the weights of the parameterized function, we can create a loss function \(l(f_{w}(x), y)\) that compares how costly our prediction was from the correct output.

This loss function can be represented as \(Q(z_{i}, w_{t})\) where \(z_{i}\) is the ith training pair, and \(w_{t}\) are the weights at timestep \(t\).

SGD says that you can update the weights of the function using a single training pair producing

\[w_{t+1} = w_{t} - \gamma_{t} \nabla_{w}Q(z_{i},w_{t})\]

effectively allowing us to optimize our weights a single randomly sampled training example at a time

What are Risks?

Ultimately, we want to minimize loss.

Ideally this loss would be some measure of accuracy over the entire unknown distribution \(dP(z)\)

If we could do this, we end up with Expected Risk

\[E(f) = \int l(f(x), y)dP(z)\]

However, we often do not know the entire distribution, we only have a subset of examples, our Training Set.

Minimizing loss over a Training Set is the Empirical Risk

\[E_{n}(f) = \frac{1}{n}\sum^{n}_{i=1}l(f(x_{i}), y_{i})\]

The hope is that the Empirical Risk is a good approximation of the Expected Risk and thus reducing loss in the Empirical should give a reduction in loss on the Expected.

How does Gradient Decent and Stochastic Gradient Decent work with Risks?

Gradient Decent is able to reach the Empirical Optimum under sufficient assumptions on the learning rate, optimization, etc.

SGD needs the same assumptions as Gradient Decent, but also needs decaying learning rates to cope with the noise in the gradient approximations.

Because of these assumptions and the noise SGD makes, it can take longer for SGD to reach the Empirical Optimum.

So… Why use SGD?

When tasks are sufficiently large and computationally bound its usually better to get within some threshold of the Empirical Optimum

\[E_{n}(\tilde{f}_{n}) < E_{n}(f_{n}) + p\]

(where \(p\) is the extra risk you are willing to accept to decrease training time)

Now we have set a predefined accuracy that we want our algorithm to reach, the error between our predefined accuracy and the best possible accuracy we could ever get is called Excess Error

\[\mathcal{E} = \mathbb{E} [E(\tilde{f}_{n}) - E(f^{*})]\]

The authors found that SGD is quicker to reach a predefined Excess Error

With sufficient training samples, you can model the Expected Risk (the actual distribution) more accurately, and be able to approach some predefined value of Expected Risk quicker with SGD than GD can.

Does 2nd Order Stochastic Gradient Decent (2SGD) have any benefits?

\[w_{t+1} = w_{t} - \Gamma_{t}\frac{1}{n}\sum^{n}_{i=1}\nabla_{w}Q(z_{i},w_{t})\]

The only difference between SGD is \(\Gamma_{t}\) which approaches the inverse of the Hessian of the cost (and is very expensive)

2SGD, with sufficient assumptions (convexity and regularity), will approach optimum solution as quickly as possible

However, 2SGD requires a large dense matrix that is too computationally expense to compute

In order to overcome the matrix, SGDQN and Averaged Stochastic Gradient Descent (ASGD) attempt to workaround it.

Both SQDQN and ASGD have nice properies and can converge faster than SGD, but still come at a significant cost (ASGD requires 2 weight matrices)

How well does the paper perform?

SGD is used quite often now, so it did become quite popular

The authors showed how SGD can be applied to various ML tasks beyond Perceptrons including K-Means, SVM, and Lasso

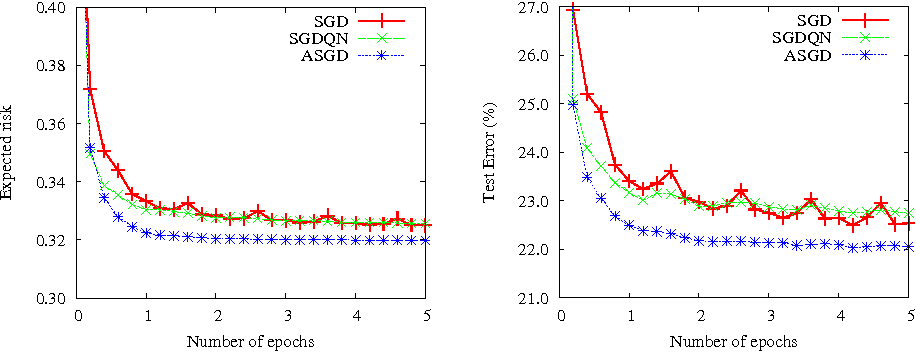
The authors tested SGD, ASGD, and SGDQN on various types of datasets showing that Stochastic Gradient Decent is capable of the Expected Risk quickly beating out other algorithms (30s -> 2.3s)

SGD vs ASGD vs SGDQN

Interesting Variants

The authors further break down the Excess Error term into

You can then choose, specific to your problem, which of these risks to minimize

In some cases GD may be the better option than SGD if you are working on a smaller machine learning problem.

TL;DR