author:	dalmeraz
score:	5 / 10

Goal:

Clarify vague intuitions about batch normalization through experimentation.

Background

Normalizing input data is good and batch normalization extends this concept to intermediate layers. Doing this on batches allows for significant speed up and produces better results, however no one understands fully why this works.

Batch Norm and Learning Rate

Activation and gradients in deep networks without batch normalization are heavy tailed which causes exploding means and variences within the model, specifically in later layers. Through analysis it is found that this “exploding” causes diverging loss.

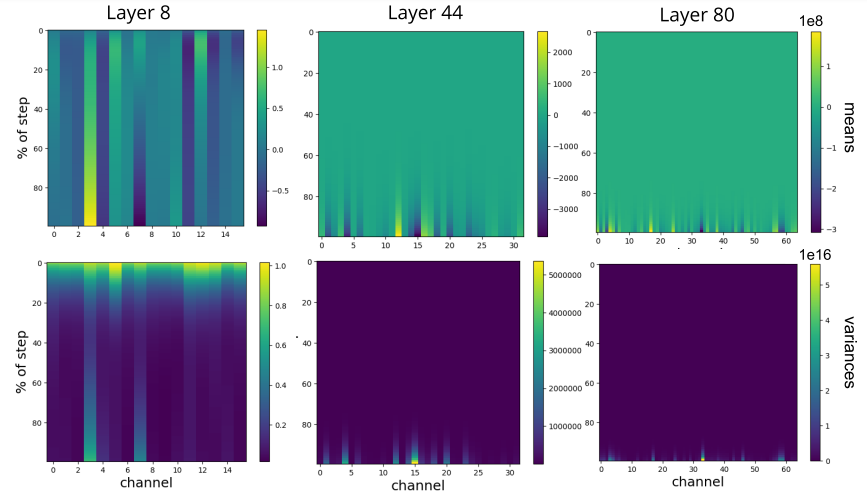
This heavy tail was visualized through the following plot which shows the magnitude of gradients when first starting to train a model:

The solution to this is using small learning rates, however using small learning rates causes the issues of:

• Training makes slow progress with flat gradients
• Model is more likely to converge in sharp local minima

Batch norm does not have a need to use small learning rates since it “corrects” values and thus avoids the issues of small learning rates.

This theory was further tested with several models that varied with batch norm and no batch norm.

Test details:

• Data: CIFAR 10 with augmentation and preprocessing
• Model: 110 layer Resnet
• Optimizer: SGD with momentum and weight decay
• Learning rate: Decrease when learning slows

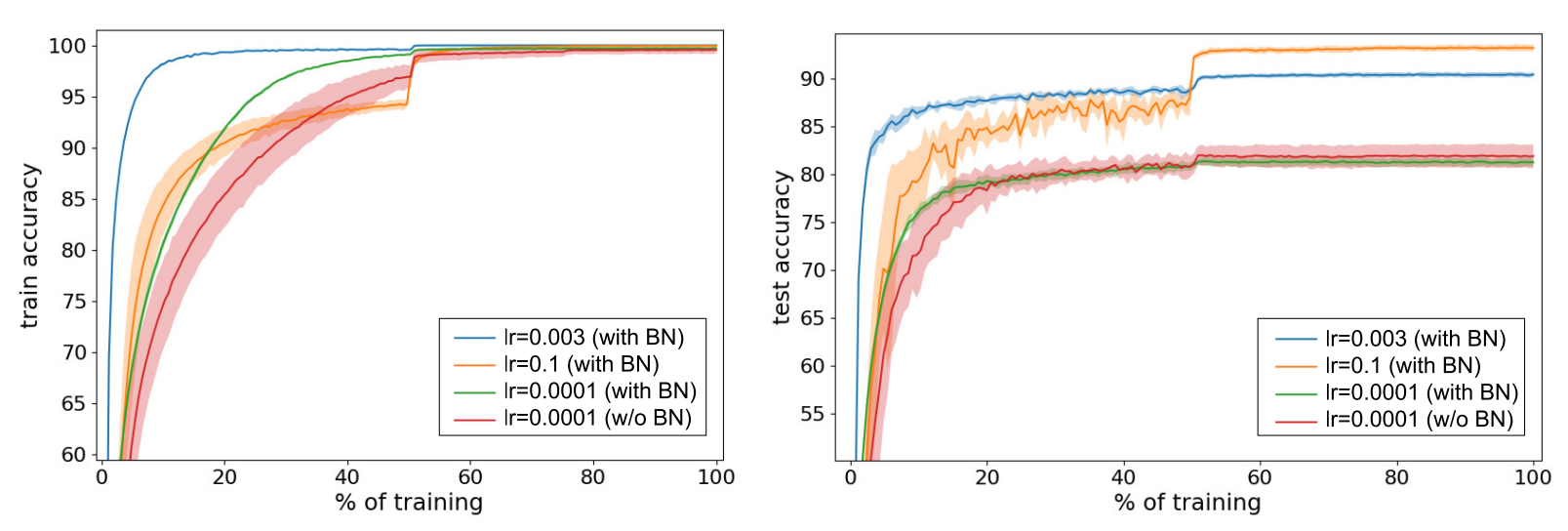
The model achieves the same accuracy with and without batch normalization in low learning rates, however since we can use high learning rates with batch normalization, we are able to get better results. Thus, the paper argues that batch normalization’s reason for success is due to the power of being able to use bigger learning rates. They further elaborate on this theoretically by speaking about a gradient’s upper bounds of noise when given by SGD:

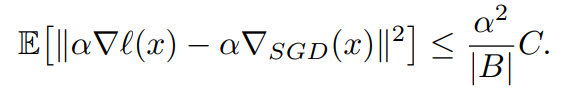
Where:

• Alpha Delta l(x) is the predicted gradient
• Alpha Delta SGD(x) is the true gradient
• Alpha is the learning rate
• B is the set of samples examples
• C is the noise quantity of a single gradient estimate

The key principle here is that an increase in the learning rate also increases the noise generated by our model. This is important because it has previously been explored that noise within SGD is important in the role of regularizing networks. So in summary, higher learning rates:

• Avoids getting stuck in short minima
• Makes quicker progress through flat gradients
• Increases important gradient noise within neural networks

As we look at gradients we also see that changes in step size causes divergences (indicated by the increase of loss) more aggressively without batch norm.

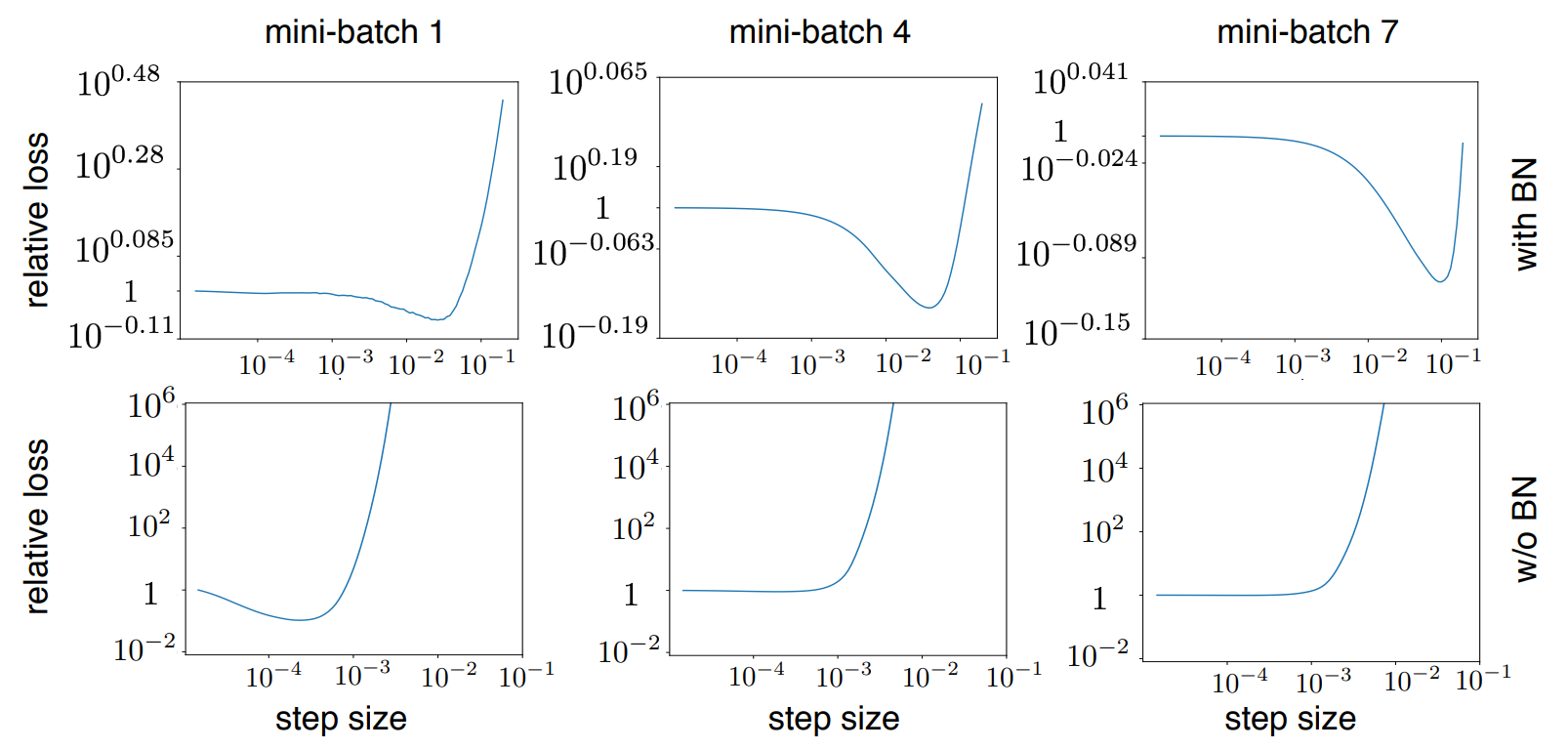
This divergence in result causes the neural networks without batch normalization to have means and variances that explode in later layers. Batch normalization fixes this by correcting the means and variances and not allowing them to explode. It was also empirically analyzed that this effect of batch normalization is so crucial to gradients that even just adding batch normalization to the final layer of the model captures 2/3rds of the overall batch normalization improvement.

Random intialization’s Effect on Gradient Explosions

The paper also explores that weaknesses in models that are fixed by batch normalization is initialization. If we multiply M, N*N gaussian matrices, we get a “blown up” singular value distribution as we reach the origin, which only becomes more aggressive as we increase M. This can be seen as emulating a neural network’s weight matrices, and can show how this causes gradient explosion as networks become deeper:

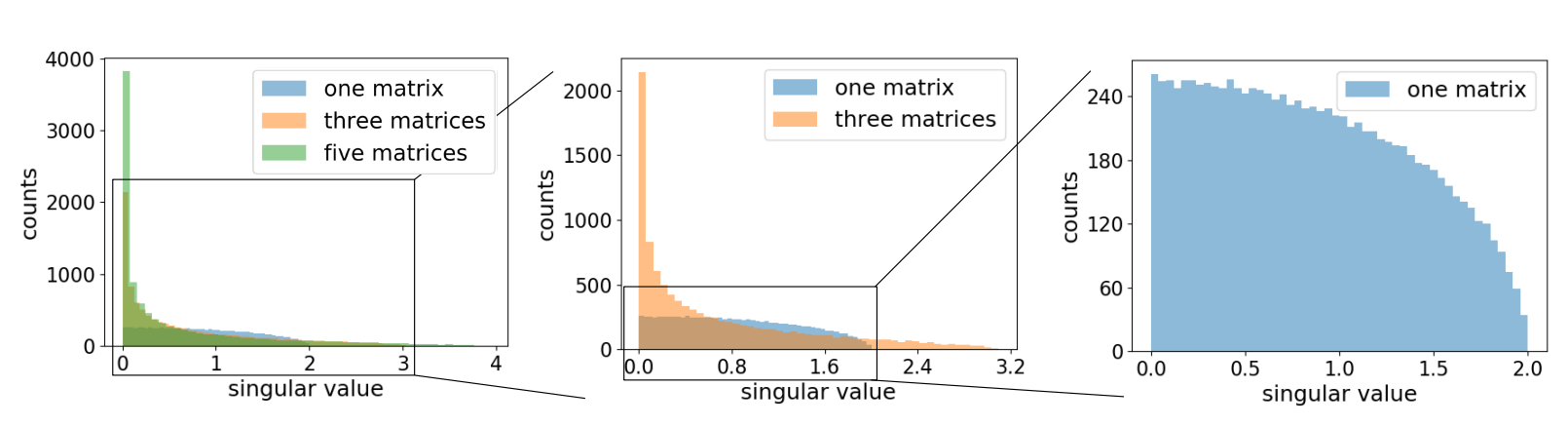
Since the proportion between large and singular values increases drastically with depth, this strongly encourages models to undergo gradient explosion if there is no batch normalization. batch normalization fixes this issues by resetting the scale of values as matrix multiplications are looped. This is supported by the correlation that smaller Resnet models can use larger learning rates.

TL;DR

• Small learning rates cause issues due to converging in sharp minima and slow progress with flat gradients
• Large learning rates causes divergence due to exploding gradients but batch norm eliminates this problem
• Random initialization naturally causes gradient explosion (if no batch normalization is used)